题目内容
9.不等式组$\left\{\begin{array}{l}-1≤x≤1\\ 0≤y≤2\end{array}\right.$表示的点集M,不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{y≥2{x}^{2}}\end{array}\right.$表示的点集记为N,在M中任取一点P,则P∈N的概率为( )| A. | $\frac{5}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{9}{16}$ | D. | $\frac{5}{16}$ |
分析 求出面积,利用几何概型的公式解答.
解答 解:不等式组$\left\{\begin{array}{l}-1≤x≤1\\ 0≤y≤2\end{array}\right.$表示的点集M,对应的区域面积为2×2=4,N对应的区域面积为${∫}_{-\frac{1}{2}}^{1}$(x+1-2x2)dx=($\frac{1}{2}$x2+x-$\frac{2}{3}$x3)|${|}_{-\frac{1}{2}}^{1}$=$\frac{9}{8}$,
由几何概型公式得,在M中任取一点P,则P∈N的概率为$\frac{9}{32}$.
故选:B.
点评 本题考查了几何概型的公式的运用,关键是求出区域面积,利用几何概型公式求值.

练习册系列答案
相关题目
19.若f(x)=sin3x+acos2x在(0,π)上存在最小值,则实数a的取值范围是( )
| A. | (0,$\frac{3}{2}$) | B. | (0,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,+∞) | D. | (0,+∞) |
14.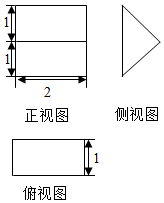 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )
 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )| A. | 2 | B. | 4 | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
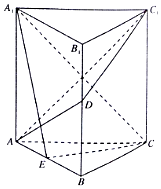 如图,正三棱柱ABC-A1B1C1的所有棱长均为2,D为棱BB1上一点,E是AB的中点.
如图,正三棱柱ABC-A1B1C1的所有棱长均为2,D为棱BB1上一点,E是AB的中点.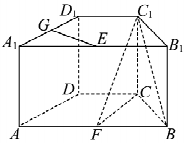 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分别是棱A1B1、AB、A1D1的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分别是棱A1B1、AB、A1D1的中点.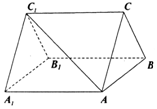 如图所示的三棱柱中,侧面ABB1A1为边长等于2的菱形,且∠AA1B1=60°,△ABC为等边三角形,面ABC⊥面ABB1A1.
如图所示的三棱柱中,侧面ABB1A1为边长等于2的菱形,且∠AA1B1=60°,△ABC为等边三角形,面ABC⊥面ABB1A1.