题目内容
7．双曲线$\frac{x^2}{16}-\frac{y^2}{9}=-1$的渐近线方程为（ ）| A． | $y=±\frac{3}{4}x$ | B． | $y=±\frac{4}{3}x$ | C． | $y=±\frac{16}{9}x$ | D． | $y=±\frac{9}{16}x$ |
分析 利用双曲线方程，直接求解双曲线的渐近线方程即可．
解答 解：双曲线$\frac{x^2}{16}-\frac{y^2}{9}=-1$的渐近线方程为：$y=±\frac{3}{4}x$．
故选：A．
点评 本题考查双曲线的简单性质的应用，渐近线方程的求法，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
17．已知函数f（x）=x2，x∈[2m，m+6]是偶函数，则实数m的值为（ ）
| A． | -4 | B． | -2 | C． | -1 | D． | 6 |
18．已知互不重合的直线l，m，互不重合的平面α，β，给出下列四个命题，错误的命题是（ ）
| A． | 若l∥α，l∥β，α∩β=m，则l∥m | B． | 若α⊥β，l⊥α，m⊥β则l⊥m | ||
| C． | 若α⊥β，α⊥γ，β∩γ=l，则l⊥α | D． | 若α∥β，l∥α，则l∥β |
2．已知$\overrightarrow a=（{1，2}），\overrightarrow b=（{m，1}）$，若$\overrightarrow a⊥\overrightarrow b$，则m=（ ）
| A． | $-\frac{1}{2}$ | B． | -2 | C． | $\frac{1}{2}$ | D． | 2 |
12．已知函数f（x）=x3+2x-8的零点用二分法计算，附近的函数值参考数据如表所示：
则方程x3+2x-8=0的近似解可取为（精确度0.1）（ ）
| x | 1 | 2 | 1.5 | 1.75 | 1.625 | 1.6875 |
| f（x） | -5.00 | 4.00 | -1.63 | 0.86 | -0.46 | 0.18 |
| A． | 1.50 | B． | 1.66 | C． | 1.70 | D． | 1.75 |
19．若f（x）=sin3x+acos2x在（0，π）上存在最小值，则实数a的取值范围是（ ）
| A． | （0，$\frac{3}{2}$） | B． | （0，$\frac{3}{2}$] | C． | [$\frac{3}{2}$，+∞） | D． | （0，+∞） |
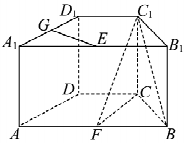如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD为等腰梯形，AB∥CD，AB=4，BC=CD=2，AA1=2，E、F、G分别是棱A1B1、AB、A1D1的中点．