题目内容
1．若双曲线$E：\frac{x^2}{9}-\frac{y^2}{16}=1$的左、右焦点分别为F1、F2，点P在双曲线E上，且|PF1|=5，则|PF2|等于（ ）| A． | 1或11 | B． | 1 | C． | 11 | D． | 13 |
分析 求得双曲线的a=3，由双曲线的定义可得||PF1|-|PF2||=2a=6，代入已知条件解方程即可得到所求值．
解答 解：双曲线$E：\frac{x^2}{9}-\frac{y^2}{16}=1$的a=3，
由双曲线的定义可得||PF1|-|PF2||=2a=6，
由|PF1|=5，可得|5-|PF2||=6，
解得|PF2|=11（-1舍去）．
故选：C．
点评 本题考查双曲线的定义和方程，考查定义法的运用，以及运算能力，属于基础题．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
相关题目
如图，在四棱锥S-ABCD中，所有侧棱长与底面边长均相等，E为SC的中点．求证：
如图，四棱锥P-ABCD的底面为正方形，PA⊥底面ABCD，PA=AD．E，F分别为底边AB和侧棱PC的中点．
16．以下有关命题的说法错误的是（ ）
| A． | 命题“若x2-3x+2=0，则 x=1”的逆否命题为“若x≠1，则 x2-3x+2≠0 | |
| B． | “x=1”是“x2-3x+2=0”的充分不必要条件 | |
| C． | 若 p∧q为假命题，则p，q均为假命题 | |
| D． | 对于命题 p：?x∈R使得x2+x+1＜0，则￢p：?x∈R，均有x2+x+1≥0 |
6．已知双曲线$M：\frac{y^2}{a^2}-\frac{x^2}{b^2}=1（{a＞0，b＞0}）$与抛物线$y=\frac{1}{8}{x^2}$有公共焦点F，F到M的一条渐近线的距离为$\sqrt{3}$，则双曲线方程为（ ）
| A． | $\frac{x^2}{7}-\frac{y^2}{3}=1$ | B． | $\frac{y^2}{3}-\frac{x^3}{7}=1$ | C． | $\frac{x^2}{3}-{y^2}=1$ | D． | ${y^2}-\frac{x^2}{3}=1$ |
13．已知函数f（x）=$\left\{\begin{array}{l}{（2a-1）x+a（x＜2）}\\{lo{g}_{a}（x-1）（x≥2）}\end{array}\right.$是R上的减函数，则实数a的取值范围是（ ）
| A． | [$\frac{1}{3}$，$\frac{1}{2}$） | B． | [$\frac{2}{5}$，$\frac{1}{2}$） | C． | [$\frac{2}{5}$，1） | D． | （0，$\frac{1}{2}$） |
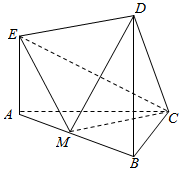如图所示的几何体中，EA⊥平面ABC，BD⊥平面ABC，AC=BC=BD=2AE=$\frac{{\sqrt{2}}}{2}AB$，M是AB的中点．