题目内容
16.以下有关命题的说法错误的是( )| A. | 命题“若x2-3x+2=0,则 x=1”的逆否命题为“若x≠1,则 x2-3x+2≠0 | |
| B. | “x=1”是“x2-3x+2=0”的充分不必要条件 | |
| C. | 若 p∧q为假命题,则p,q均为假命题 | |
| D. | 对于命题 p:?x∈R使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1≥0 |
分析 ①根据逆否命题的定义进行判断.
②根据充分条件和必要条件的定义进行判断
③根据复合命题的真假关系进行判断.
④根据含有量词的命题的否定进行判断.
解答 解:A.命题“若x2-3x+2=0,则 x=1”的逆否命题为“若x≠1,则 x2-3x+2≠0”,故A正确,
B.由x2-3x+2=0得x=1或x=1,则“x=1”是“x2-3x+2=0”的充分不必要条件,故B正确,
C.若 p∧q为假命题,则p,q至少有一个为假命题,故C错误,
D.命题 p:?x∈R使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1≥0,正确故D正确.
故错误的是C,
故选:C.
点评 本题主要考查命题的真假判断,涉及四种命题真假关系,含有量词的命题的否定以及充分条件和必要条件的判断,综合性较强,但难度不大.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
3.某学校采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做视力检查,现将800名学生从1到800进行编号,已知从49~64这16个数中被抽到的数是58,则在第2小组17~32中被抽到的数是( )
| A. | 23 | B. | 24 | C. | 26 | D. | 28 |
4.设m.n是两条不同的直线,α是一个平面,下列命题中正确的是( )
| A. | 若m⊥n,n?α,则m⊥α | B. | 若m∥α,n∥α,则m∥n | C. | 若m⊥α,m⊥n,则n∥α | D. | m⊥α,m∥n,则n⊥α |
11.“a,b是异面直线”是指( )
| A. | a?平面a,b?平面β且α∩β=∅ | B. | a?平面α,b?平面α | ||
| C. | a?平面α,b?平面β | D. | a∩b=∅且a不平行于b |
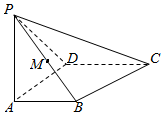 四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=AB=$\frac{1}{2}$CD=1,M为PB的中点,求直线CM与平面ABCD所成角的正弦值.
四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=AB=$\frac{1}{2}$CD=1,M为PB的中点,求直线CM与平面ABCD所成角的正弦值.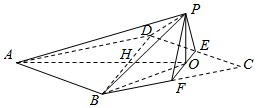 边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.
边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.