题目内容
13．已知函数f（x）=$\left\{\begin{array}{l}{（2a-1）x+a（x＜2）}\\{lo{g}_{a}（x-1）（x≥2）}\end{array}\right.$是R上的减函数，则实数a的取值范围是（ ）| A． | [$\frac{1}{3}$，$\frac{1}{2}$） | B． | [$\frac{2}{5}$，$\frac{1}{2}$） | C． | [$\frac{2}{5}$，1） | D． | （0，$\frac{1}{2}$） |
分析 由分段函数的性质结合一次函数和对数函数的单调性，列出不等式组，由此能求出实数a的取值范围．
解答 解：∵函数f（x）=$\left\{\begin{array}{l}{（2a-1）x+a（x＜2）}\\{lo{g}_{a}（x-1）（x≥2）}\end{array}\right.$是R上的减函数，
∴$\left\{\begin{array}{l}{2a-1＜0}\\{0＜a＜1}\\{lo{g}_{a}（2-1）≤2（2a-1）+a}\end{array}\right.$，
解得$\frac{2}{5}≤a＜\frac{1}{2}$．
∴实数a的取值范围是[$\frac{2}{5}$，$\frac{1}{2}$）．
故选：B．
点评 本题考查满足条件的实数的取值范围的求法，是中档题，解题时要认真审题，注意分段函数的性质的合理运用．
练习册系列答案
小学课时特训系列答案
相关题目
4．设m．n是两条不同的直线，α是一个平面，下列命题中正确的是（ ）
| A． | 若m⊥n，n?α，则m⊥α | B． | 若m∥α，n∥α，则m∥n | C． | 若m⊥α，m⊥n，则n∥α | D． | m⊥α，m∥n，则n⊥α |
1．若双曲线$E：\frac{x^2}{9}-\frac{y^2}{16}=1$的左、右焦点分别为F1、F2，点P在双曲线E上，且|PF1|=5，则|PF2|等于（ ）
| A． | 1或11 | B． | 1 | C． | 11 | D． | 13 |
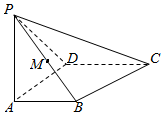四棱锥P-ABCD中，AB⊥AD，AD⊥DC，PA⊥底面ABCD，PA=AD=AB=$\frac{1}{2}$CD=1，M为PB的中点，求直线CM与平面ABCD所成角的正弦值．
如图，三棱柱ABC-A1B1C1中，AA1⊥平面ABC，BC⊥AC，BC=AC=2，AA1=3，D为AC的中点．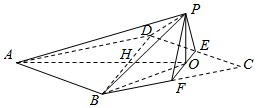 
边长为4的菱形ABCD中，满足∠DCB=60°，点E，F分别是边CD和CB的中点，AC交BD于点H，AC交EF于点O，沿EF将△CEF翻折到△PEF的位置，使平面PEF⊥平面ABD，连接PA，PB，PD，得到如图所示的五棱锥P-ABFED．
3．在数列{an}中，已知${S_n}={2^n}-1$，则a12+a22+…+an2等于（ ）
| A． | $\frac{{4}^{n}-1}{3}$ | B． | $\frac{（{2}^{n}-1）^{2}}{3}$ | C． | 4n-1 | D． | （2n-1）2 |