题目内容
已知曲线y=
x3,求曲线在点P(3,9)处的切线方程.
| 1 |
| 3 |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:根据导数的几何意义求出函数在x=3处的导数,从而得到切线的斜率,再利用点斜式方程写出切线方程即可.
解答:
解:曲线y=
x3,y'=x2
y'|x=3=9.
而切点的坐标为(3,9)
∴曲线y=
x3在点P(3,9)处的切线方程为:y-9=9(x-3),即9x-y-18=0.
故答案为:9x-y-18=0.
| 1 |
| 3 |
y'|x=3=9.
而切点的坐标为(3,9)
∴曲线y=
| 1 |
| 3 |
故答案为:9x-y-18=0.
点评:本题主要考查了利用导数研究曲线上某点切线方程,考查运算求解能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数f(x)=
的值域为R,则m的取值范围是( )
| x |
| mx2+mx+1 |
| A、[0,4] |
| B、(-∞,0) |
| C、(-∞,0] |
| D、(-∞,0]∪[4,+∞) |
在△ABC中,角A,B,C所对的边分别是a,b,c,若
-
+1=0,则角B的度数是( )
| tanB |
| tanC |
| 2a |
| c |
| A、60° | B、120° |
| C、150° | D、60°或120° |
已知向量
=(-a,2,1)与
=(1,2a,-3)垂直,则a等于( )
| m |
| n |
| A、2 | B、-2 | C、1 | D、-1 |
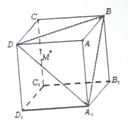 如图,在棱长为1的正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m,n,p分别是点M到平面ADD1A1,平面ABB1A1,平面ABCD的距离,若f(M)=(
如图,在棱长为1的正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m,n,p分别是点M到平面ADD1A1,平面ABB1A1,平面ABCD的距离,若f(M)=(