题目内容

设P为△ABC內的一点，且
AP
=
2
5
AB
+
1
5
AC
．
（1）求△PBC与△ABC的面积之比；
（2）设
PA
=x
PB
+y
PC
，求实数x，y的值．
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：（1）如图所示，设
AM
=
2
5
AB
，
AN
=
1
5
AC
．由MP∥AC，可得
CF
CB
=
2
5
，同理可得
BE
BC
=
1
5
，可得
EF
BC
=
2
5
．得到
FP
CN
=
1
2
，即可得出
DP
DA
=
PF
AC
=
2
5
．进而得到△PBC与△ABC的面积之比；
（2）利用向量的三角形法则可得：
PB
=
PA
+
AB
，
PC
=
PA
+
AC
，可得
PA
=
x
1-x-y
AB
+
y
1-x-y
AC
，与
AP
=
2
5
AB
+
1
5
AC
比较即可得出．
解答： 解：（1）如图所示，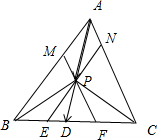
设
AM
=
2
5
AB
，
AN
=
1
5
AC
．
∵MP∥AC，∴
CF
CB
=
2
5
，
同理可得
BE
BC
=
1
5
，
∴
EF
BC
=
2
5
．
∴
FP
CN
=
1
2
，
∴
DP
DA
=
PF
AC
=
2
5
．
∴△PBC与△ABC的面积之比=
2
5
；
（2）∵
PB
=
PA
+
AB
，
PC
=
PA
+
AC
，
∴
PA
=x
PB
+y
PC
=x(
PA
+
AB
)+y(
PA
+
AC
)，
∴
PA
=
x
1-x-y
AB
+
y
1-x-y
AC
，
与
AP
=
2
5
AB
+
1
5
AC
比较可得：
x
1-x-y
=-
2
5
y
1-x-y
=-
1
5
，解得
x=-1
y=-
1
2
．
点评：本题考查了向量的三角形法则、平行四边形法则、平行线分线段成比例定理、共面向量基本定理，考查了推理能力和计算能力，属于难题．
练习册系列答案
相关题目
已知非零向量
a
，
b
，满足|
a
|=1且（
a
-
b
）•（
a
+
b
）=
1
2
．
（1）若
a
•
b
=
1
2
，求向量
a
，
b
的夹角；
（2）在（1）的条件下，求|
a
-
b
|的值．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左，右焦点分别为F1，F2，上顶点为B．Q为抛物线y2=12x的焦点，且
F1B
•
QB
=0，2
F1F2
+
QF1
=0．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）过定点P（0，2）的直线l与椭圆C交于M，N两点（M在P，N之间），设直线l的斜率为k（k＞0），在x轴上是否存在点A（m，0），使得以AM，AN为邻边的平行四边形为菱形？若存在，求出实数m的取值范围；若不存在，请说明理由．
已知二次函数f（x）满足：
①在x=1时有极值；
②图象过点（0，3），且在该点处的切线与直线2x+y=0平行．
（1）求f（x）的解析式；
（2）求函数g（x）=f（x2）在[-2，2]上的最大值和最小值．
如图，设双曲线C1：
y2
a2
-
x2
b2
=1（a＞0，b＞0）的上焦点为F，上顶点为A，点B为双曲线虚轴的左端点，已知Cl的离心率为
2
3
3
，且△ABF的面积S=1-
3
2
．
（Ⅰ）求双曲线Cl的方程；
（Ⅱ）设抛物线C2的顶点在坐标原点，焦点为F，动直线l与C2相切于点P，与C2的准线相交于点Q试推断以线段PQ为直径的圆是否恒经过y轴上的某个定点M？若是，求出定点M的坐标；若不是，请说明理由．
甲、乙两名篮球运动员，投篮的命中率分别为0.7与0.8．
（1）如果每人投篮一次，求甲、乙两人至少有一人进球的概率；
（2）如果每人投篮三次，求甲投进2球且乙投进1球的概率．
已知函数f（x）=alnx+x2（a为常实数）．
（1）若a=-2，求函数f（x）的单调区间；
（2）若当x∈[1，e]时，f（x）≤a+2恒成立，求实数a的取值范围；
（3）求函数f（x）在[1，e]上的最小值及相应的x值．
已知函数f（x）=x-
1
x
．
（1）判断函数f（x）的奇偶性，并加以证明；
（2）用定义证明函数f（x）在区间[1，+∞）上为增函数；
（3）若函数f（x）在区间[2，a]上的最大值与最小值之和不小于
11a-2
2a
，求a的取值范围．
函数y=
7x-3
x
在[
1
2
，3]上的最小值是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网