题目内容
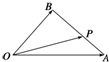
如图，A，B是圆O上的两点，且OA⊥OB，OA=2，C为OA的中点，连接BC并延长交圆O于点D，则CD=考点：与圆有关的比例线段
专题：选作题,立体几何
分析：由题设条件推导出OC=CA=1，OB=2，BC=
，由相交弦定理得（2+1）•（2-1）=BC•CD，由此能求出CD．
| 5 |
解答：
解：
如图，∵A，B是圆O上的两点，且OA⊥OB，OA=2，
C为OA的中点，连接BC并延长交圆O于点D，
∴OC=CA=1，OB=2，
∴BC=
，
∴由相交弦定理得（2+1）•（2-1）=BC•CD，
∴CD=
．
故答案为：
．
如图，∵A，B是圆O上的两点，且OA⊥OB，OA=2，C为OA的中点，连接BC并延长交圆O于点D，
∴OC=CA=1，OB=2，
∴BC=
| 5 |
∴由相交弦定理得（2+1）•（2-1）=BC•CD，
∴CD=
3
| ||
| 5 |
故答案为：
3
| ||
| 5 |
点评：本题考查与圆相关的线段长的求法，是中档题．熟练掌握相交弦定理是解题的关键．
练习册系列答案
相关题目
已知函数y=f（x）在x=x0处可导，若
=-
，则f′（x0）等于（ ）
| lim |
| k→0 |
| f(x0-k)-f(x0) |
| 2k |
| 1 |
| 4 |
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
