题目内容
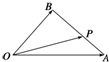
如图，在△OAB中，P为线段AB上的一点，
=x
+y
，且
=2
，则x= ，y= ．
| OP |
| OA |
| OB |
| BP |
| PA |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：由
=2
，利用向量三角形法则可得
-
=2(
-
)，再利用向量基本定理即可得出．
| BP |
| PA |
| OP |
| OB |
| OA |
| OP |
解答：
解：∵
=2
，
∴
-
=2(
-
)，
化为
=
+
，
与
=x
+y
比较可得：x=
，y=
．
故答案分别为：
；
．
| BP |
| PA |
∴
| OP |
| OB |
| OA |
| OP |
化为
| OP |
| 2 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
与
| OP |
| OA |
| OB |
| 2 |
| 3 |
| 1 |
| 3 |
故答案分别为：
| 2 |
| 3 |
| 1 |
| 3 |
点评：本题考查了向量三角形法则、向量基本定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
如图，A，B是圆O上的两点，且OA⊥OB，OA=2，C为OA的中点，连接BC并延长交圆O于点D，则CD=若
＜θ＜
，则下列不等式成立的是（ ）
| π |
| 4 |
| π |
| 3 |
| A、sinθ＞cosθ＞tanθ |
| B、cosθ＞tanθ＞sinθ |
| C、sinθ＞tanθ＞cosθ |
| D、tanθ＞sinθ＞cosθ |