题目内容
7.设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的焦点为F1和F2,P是椭圆上任一点,若∠F1PF2的最大值为$\frac{2π}{3}$,则此椭圆的离心率为$\frac{\sqrt{3}}{2}$.分析 由椭圆的性质可得:当点P取椭圆短轴的一个端点时,∠F1PF2取得最大值为$\frac{2π}{3}$,可得tan∠OPF2=tan$\frac{π}{3}$=$\sqrt{3}$=$\frac{c}{b}$,化简整理即可得出.
解答 解:由椭圆的性质可得:当点P取椭圆短轴的一个端点时,∠F1PF2取得最大值为$\frac{2π}{3}$,
∴tan∠OPF2=tan$\frac{π}{3}$=$\sqrt{3}$=$\frac{c}{b}$,
∴c2=3b2=3(a2-c2),
∴$\frac{{c}^{2}}{{a}^{2}}$=$\frac{3}{4}$,
解得e=$\frac{c}{a}$=$\frac{{\sqrt{3}}}{2}$,
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查了椭圆的标准方程及其性质、直角三角形的边角关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知实数a,b满足log2a+log2b=-2,则a+b的最小值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 4 |
12.复数z=-3+(1+i)2在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.已知全集U={e,lne,ln1},集合A={1,0},则∁UA=( )
| A. | {e,lne} | B. | {e} | C. | {e,lne2} | D. | {lne,lne2} |
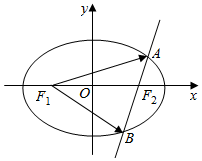 已知椭圆C的中心在原点,焦点F1,F2在x轴上,离心率e=$\frac{1}{2}$,且经过点M(1,$\frac{3}{2}$).
已知椭圆C的中心在原点,焦点F1,F2在x轴上,离心率e=$\frac{1}{2}$,且经过点M(1,$\frac{3}{2}$).