题目内容
19.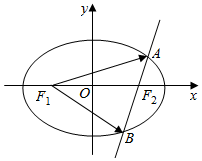 已知椭圆C的中心在原点,焦点F1,F2在x轴上,离心率e=$\frac{1}{2}$,且经过点M(1,$\frac{3}{2}$).
已知椭圆C的中心在原点,焦点F1,F2在x轴上,离心率e=$\frac{1}{2}$,且经过点M(1,$\frac{3}{2}$).(1)求椭圆C的方程;
(2)若直线l经过椭圆C的右焦点F2,且与椭圆C交于A,B两点,使得$\overrightarrow{{F_1}A}•\overrightarrow{{F_1}B}$=1,求直线l的方程.
分析 (1)设椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,由离心率$e=\frac{1}{2}$,且经过点$M({1,\frac{3}{2}})$,能求出a2=4,b2=3,由此能求出椭圆C的方程.
(2)设直线l的方程为y=k(x-1),代入椭圆C的方程,得(3+4k2)x2-8k2x+4k2-12=0,由此利用韦达定理、向量的数量积,结合已知条件能求出直线l的方程.
解答 解:(1)设椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,
由题意得$e=\frac{c}{a}=\frac{1}{2}$且$\frac{1}{a^2}+\frac{9}{{4{b^2}}}=1$,
解得a2=4,b2=3,
所以椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$;
(2)设直线l的方程为y=k(x-1),代入椭圆C的方程$\frac{x^2}{4}+\frac{y^2}{3}=1$,
化简得(3+4k2)x2-8k2x+4k2-12=0,设A(x1,y1),B(x2,y2),
则${x_1}+{x_2}=\frac{{8{k^2}}}{{3+4{k^2}}},{x_1}{x_2}=\frac{{4{k^2}-12}}{{3+4{k^2}}}$①
又${F_1}({-1,0}),\overrightarrow{{F_1}A}•\overrightarrow{{F_1}B}=({{x_1}+1,{y_1}})({{x_2}+1,{y_2}})=({{x_1}+1})({{x_2}+1})+{y_1}{y_2}$,
其中y1=k(x1-1),y2=k(x2-1).
所以$\overrightarrow{{F_1}A}•\overrightarrow{{F_1}B}=({{x_1}+1})({{x_2}+1})+{k^2}({{x_1}-1})({{x_2}-1})$
=$({1+{k^2}}){x_1}{x_2}+({1-{k^2}})({{x_1}+{x_2}})+1+{k^2}$,
把①代入上式可解得k=±2,
所以直线l的方程为y=±2(x-1).
点评 本题考查椭圆方程、直线方程的求法,是中档题,解题时要认真审题,注意椭圆性质、韦达定理、向量的数列积的性质的合理运用.

| A. | 6折 | B. | 7折 | C. | 8折 | D. | 9折 |
| A. | -8 | B. | 10 | C. | 12 | D. | 15 |
| A. | [0,$\frac{π}{2}$] | B. | [$\frac{π}{2}$,π] | C. | [$\frac{π}{8}$,$\frac{5π}{8}$] | D. | [$\frac{5π}{8}$,$\frac{9π}{8}$] |

| A. | $\frac{8π}{3}$ | B. | 3π | C. | $\frac{10π}{3}$ | D. | $\frac{11π}{3}$ |