题目内容
 在极坐标系中,已知三点O(0,0),A(2,
在极坐标系中,已知三点O(0,0),A(2,| π |
| 2 |
| 2 |
| π |
| 4 |
(Ⅰ)求经过O,A,B的圆C的极坐标方程
(Ⅱ)以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,圆C2的参数方程
|
考点:参数方程化成普通方程
专题:选作题,坐标系和参数方程
分析:(Ⅰ)设(ρ,θ)是所求圆上的任意一点,则由OP=OBcos(θ-
),求出圆的极坐标方程;
(Ⅱ)圆C1的普通方程是:(x-1)2+(y-1)2=2,圆C2的普通方程为:(x+1)2+(y+1)2=a2.圆C1与圆C2相切,分为外切的内切两种情况讨论,利用圆心距与半径之间的关系建立方程,求实数a的值.
| π |
| 4 |
(Ⅱ)圆C1的普通方程是:(x-1)2+(y-1)2=2,圆C2的普通方程为:(x+1)2+(y+1)2=a2.圆C1与圆C2相切,分为外切的内切两种情况讨论,利用圆心距与半径之间的关系建立方程,求实数a的值.
解答:
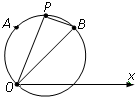 解:(Ⅰ)设(ρ,θ)是所求圆上的任意一点,
解:(Ⅰ)设(ρ,θ)是所求圆上的任意一点,
则OP=OBcos(θ-
),
故所求的圆的极坐标方程为ρ=2
cos(θ-
);
(Ⅱ)圆C1的方程为ρ=2
cos(θ-
)的直角坐标方程为:(x-1)2+(y-1)2=2,
圆心C1(1,1),半径r1=
,
圆C2的参数方程
(θ是参数)的普通方程为:(x+1)2+(y+1)2=a2.
圆心距C1C2=2
,
两圆外切时,C1C2=r1+r2=
+|a|=2
,a=±
;
两圆内切时,C1C2=|r1-r2|=|
-|a||=2
,a=±3
.
综上,a=±
或a=±3
.
 解:(Ⅰ)设(ρ,θ)是所求圆上的任意一点,
解:(Ⅰ)设(ρ,θ)是所求圆上的任意一点,则OP=OBcos(θ-
| π |
| 4 |
故所求的圆的极坐标方程为ρ=2
| 2 |
| π |
| 4 |
(Ⅱ)圆C1的方程为ρ=2
| 2 |
| π |
| 4 |
圆心C1(1,1),半径r1=
| 2 |
圆C2的参数方程
|
圆心距C1C2=2
| 2 |
两圆外切时,C1C2=r1+r2=
| 2 |
| 2 |
| 2 |
两圆内切时,C1C2=|r1-r2|=|
| 2 |
| 2 |
| 2 |
综上,a=±
| 2 |
| 2 |
点评:本题主要考查求圆的极坐标方程的方法,考查参数方程化成普通方程、简单曲线的极坐标方程、圆与圆的位置关系及其应用,属于基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 已知椭圆
已知椭圆 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上. 已知椭圆
已知椭圆