题目内容
13.为发展国外孔子学院的发展,教育部选派6名中文教师到泰国、马来西亚、缅甸任教中文,若每个国家至少去一人,则选派方案种数为540.分析 根据题意,每个国家至少去一人,可以分组为(1,2,3),(2,2,2),(1,1,4),分组后再分配,问题得意解决.
解答 解:根据题意,每个国家至少去一人,可以分组为(1,2,3),(2,2,2),(1,1,4),
分组的种数为:C63•C32+C64+$\frac{{C}_{6}^{2}{C}_{4}^{2}}{{A}_{3}^{3}}$=60+15+15=90,
分组后,再分配到三个国家,
故有90•A33=540种,
故答案为:540.
点评 本题考查排列、组合的应用,注意正确使用平均分组与不平均分组的公式.

练习册系列答案
相关题目
4.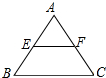 在三角形ABC中,E、F分别是AB、AC的中点,若在三角形内部,随机取一点Q,则点Q取自△AEF内部的概率是( )
在三角形ABC中,E、F分别是AB、AC的中点,若在三角形内部,随机取一点Q,则点Q取自△AEF内部的概率是( )
 在三角形ABC中,E、F分别是AB、AC的中点,若在三角形内部,随机取一点Q,则点Q取自△AEF内部的概率是( )
在三角形ABC中,E、F分别是AB、AC的中点,若在三角形内部,随机取一点Q,则点Q取自△AEF内部的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
3.已知平面α截一球面得圆M,过圆心M且与α成30°二面角的平面β截该球面得圆N.若该球面的半径为4,圆M的面积为4π,则圆N的面积为( )
| A. | 7π | B. | 9π | C. | 11π | D. | 13π |
20.在等差数列{an}中,a20l5=a2013+6,则公差d等于( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |