题目内容
(本小题满分12分)
已知函数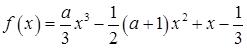 (
(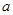
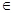 R).
R).
(1) 若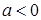 ,求函数
,求函数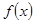 的极值;
的极值;
(2)是否存在实数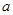 使得函数
使得函数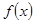 在区间
在区间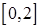 上有两个零点,若存在,求出
上有两个零点,若存在,求出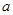 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
已知函数
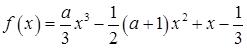 (
(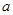
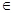 R).
R).(1) 若
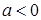 ,求函数
,求函数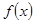 的极值;
的极值;(2)是否存在实数
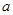 使得函数
使得函数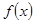 在区间
在区间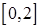 上有两个零点,若存在,求出
上有两个零点,若存在,求出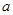 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。 (1) 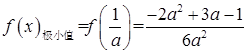 ,
,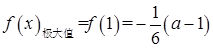 ;
;
(2)存在实数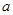 ,当
,当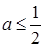 时,函数
时,函数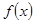 在区间
在区间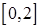 上有两个零点。
上有两个零点。
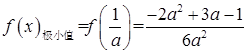 ,
,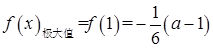 ;
;(2)存在实数
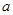 ,当
,当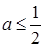 时,函数
时,函数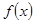 在区间
在区间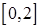 上有两个零点。
上有两个零点。本试题主要是考查了运用导数求解函数的极值以及函数的零点问题的运用
(1)先求解导数,运用导数的思想求解得到极值。
(2)假设存在实数a使得函数f=(x)在区间[0,2]上有两个零点,那么根据函数的单调性以及函数的极大值和极小值的符号,来得到参数a的范围。
解:(1)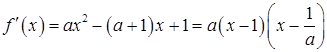 ………………1分
………………1分
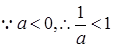 ,
,
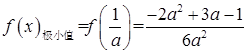 ,
,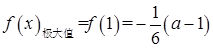 …………5分
…………5分
(2)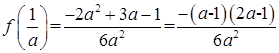 ,
,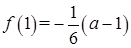
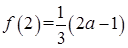 ,
, 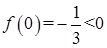
① 当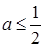 时,
时,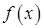 在
在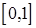 上为增函数,在
上为增函数,在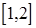 上为减函数,
上为减函数,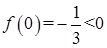 ,
,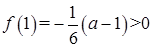 ,
,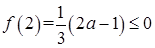 ,所以
,所以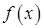 在区间
在区间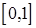 ,
,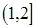 上各有一个零点,即在
上各有一个零点,即在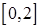 上有两个零点; ………………………7分
上有两个零点; ………………………7分
② 当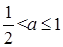 时,
时,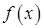 在
在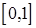 上为增函数,在
上为增函数,在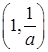 上为减函数,
上为减函数,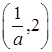 上为
上为
增函数,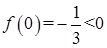 ,
,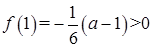 ,
,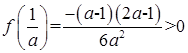 ,
,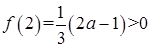 ,所以
,所以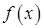 只在区间
只在区间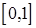 上有一个零点,故在
上有一个零点,故在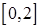 上只有一个零点; …………………………9分
上只有一个零点; …………………………9分
③ 当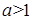 时,
时,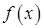 在
在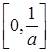 上为增函数,在
上为增函数,在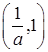 上为减函数,
上为减函数,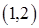 上为增函数,
上为增函数,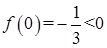 ,
,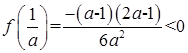 ,
,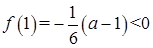 ,
,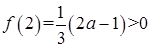 , 所以
, 所以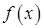 只在区间
只在区间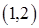 上有一个零点,故在
上有一个零点,故在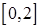 上只有一个零点; …………………………11分
上只有一个零点; …………………………11分
故存在实数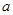 ,当
,当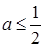 时,函数
时,函数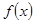 在区间
在区间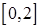 上有两个零点。……………12分
上有两个零点。……………12分
(1)先求解导数,运用导数的思想求解得到极值。
(2)假设存在实数a使得函数f=(x)在区间[0,2]上有两个零点,那么根据函数的单调性以及函数的极大值和极小值的符号,来得到参数a的范围。
解:(1)
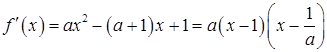 ………………1分
………………1分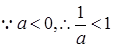 ,
,| | 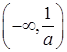 | 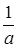 | 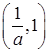 | 1 | 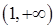 |
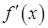 | - | 0 | + | 0 | - |
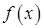 | 递减 | 极小值 | 递增 | 极大值 | 递减 |
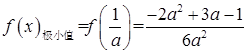 ,
,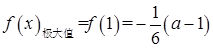 …………5分
…………5分(2)
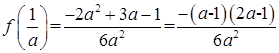 ,
,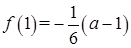
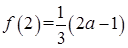 ,
, 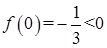
① 当
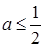 时,
时,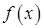 在
在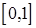 上为增函数,在
上为增函数,在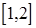 上为减函数,
上为减函数,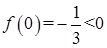 ,
,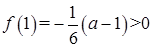 ,
,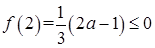 ,所以
,所以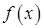 在区间
在区间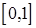 ,
,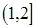 上各有一个零点,即在
上各有一个零点,即在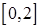 上有两个零点; ………………………7分
上有两个零点; ………………………7分② 当
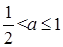 时,
时,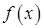 在
在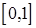 上为增函数,在
上为增函数,在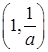 上为减函数,
上为减函数,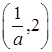 上为
上为增函数,
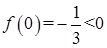 ,
,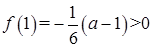 ,
,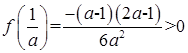 ,
,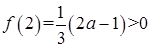 ,所以
,所以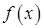 只在区间
只在区间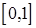 上有一个零点,故在
上有一个零点,故在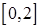 上只有一个零点; …………………………9分
上只有一个零点; …………………………9分③ 当
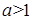 时,
时,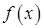 在
在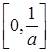 上为增函数,在
上为增函数,在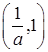 上为减函数,
上为减函数,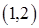 上为增函数,
上为增函数,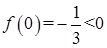 ,
,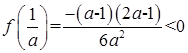 ,
,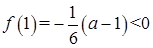 ,
,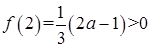 , 所以
, 所以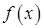 只在区间
只在区间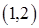 上有一个零点,故在
上有一个零点,故在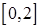 上只有一个零点; …………………………11分
上只有一个零点; …………………………11分故存在实数
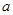 ,当
,当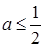 时,函数
时,函数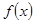 在区间
在区间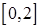 上有两个零点。……………12分
上有两个零点。……………12分
练习册系列答案
相关题目
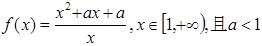
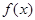 的单调性并证明;
的单调性并证明;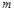 满足
满足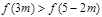 ,试确定
,试确定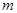 的取值范围。
的取值范围。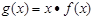 对任意
对任意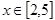 时,
时,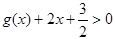 恒成立,求
恒成立,求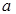 的取值范围。
的取值范围。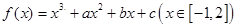 ,且函数
,且函数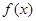 在
在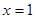 和
和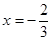 处都取得极值。
处都取得极值。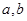 的值;
的值;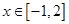 ,
,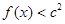 恒成立,求实数
恒成立,求实数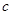 的取值范围。
的取值范围。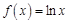 .
.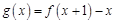 的最大值;
的最大值;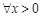 ,不等式
,不等式 恒成立,求实数
恒成立,求实数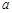 的取值范围;
的取值范围;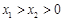 ,求证:
,求证: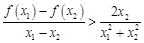 .
.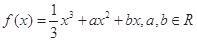
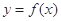 经过点P(1,2),且曲线C在点P处的切线平行于直线
经过点P(1,2),且曲线C在点P处的切线平行于直线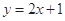 ,求
,求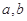 的值。
的值。 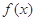 在区间(1,2)内存在两个极值点,求证:
在区间(1,2)内存在两个极值点,求证: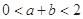
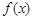 满足对于
满足对于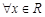 ,均有
,均有 成立.
成立.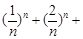 …
…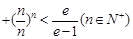 .
.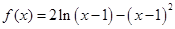 .
.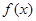 的单调递增区间;
的单调递增区间;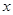 的方程
的方程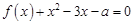 在区间
在区间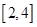 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数 的取值范围.
的取值范围. 若
若 在区间
在区间 上是减函数,则实数a的取值范围是 .
上是减函数,则实数a的取值范围是 . 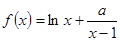 在
在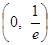 内有极值。
内有极值。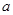 的取值范围;
的取值范围;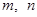 分别为
分别为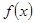 的极大值和极小值,记
的极大值和极小值,记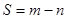 ,求S的取值范围。
,求S的取值范围。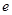 为自然对数的底数)
为自然对数的底数)