题目内容
(本题满分14分)已知函数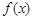 满足对于
满足对于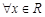 ,均有
,均有 成立.
成立.
(1)求函数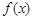 的解析式;
的解析式;
(2)求函数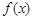 的最小值;
的最小值;
(3)证明: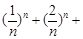 …
…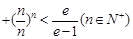 .
.
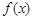 满足对于
满足对于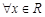 ,均有
,均有 成立.
成立.(1)求函数
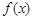 的解析式;
的解析式;(2)求函数
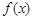 的最小值;
的最小值;(3)证明:
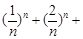 …
…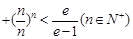 .
.(1)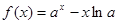 (2)1
(2)1
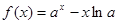 (2)1
(2)1 (1)由已知等式,用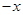 代替
代替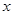 得到一个关于
得到一个关于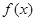 与
与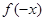 得方程组,解出
得方程组,解出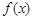 .
.
(2)用导数法求最值.(3) 在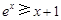 中令
中令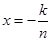 (
(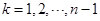 ),用放缩法证明.
),用放缩法证明.
试题分析:(1)依题意得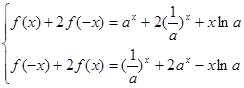 ,
,
解之得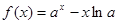 . ……4分
. ……4分
(2)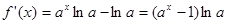 ,
,
当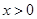 时
时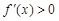 当
当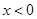 时
时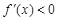 ,
,
∴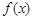 )在
)在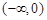 上递减在
上递减在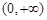 上递增,
上递增,
∴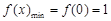 . ……8分
. ……8分
(3)由(2)得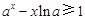 恒成立,令
恒成立,令 , 则
, 则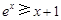 ,
,
在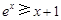 中令
中令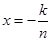 (
(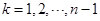 ),
),
∴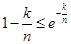 ,∴
,∴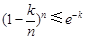 ,
,
∴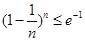 ,
, 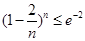 ,…,
,…,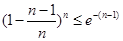 ,
,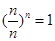 ),
),
∴

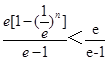 . ……14分
. ……14分
点评:(1)解方程组是要注意把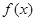 与
与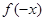 看作是两个变量.(3)要仔细分析要证明的不等式的结构,令
看作是两个变量.(3)要仔细分析要证明的不等式的结构,令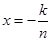 是解决问题的关键.
是解决问题的关键.
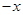 代替
代替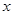 得到一个关于
得到一个关于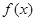 与
与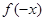 得方程组,解出
得方程组,解出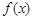 .
.(2)用导数法求最值.(3) 在
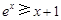 中令
中令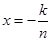 (
(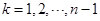 ),用放缩法证明.
),用放缩法证明.试题分析:(1)依题意得
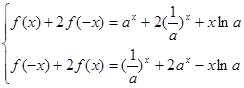 ,
,解之得
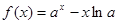 . ……4分
. ……4分(2)
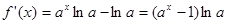 ,
,当
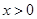 时
时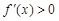 当
当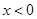 时
时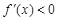 ,
,∴
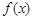 )在
)在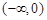 上递减在
上递减在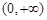 上递增,
上递增,∴
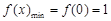 . ……8分
. ……8分(3)由(2)得
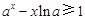 恒成立,令
恒成立,令 , 则
, 则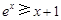 ,
,在
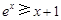 中令
中令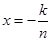 (
(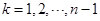 ),
),∴
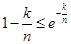 ,∴
,∴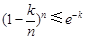 ,
,∴
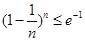 ,
, 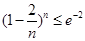 ,…,
,…,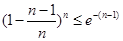 ,
,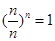 ),
),∴


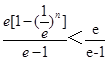 . ……14分
. ……14分点评:(1)解方程组是要注意把
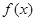 与
与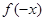 看作是两个变量.(3)要仔细分析要证明的不等式的结构,令
看作是两个变量.(3)要仔细分析要证明的不等式的结构,令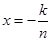 是解决问题的关键.
是解决问题的关键.
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
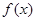 的导函数
的导函数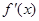 满足
满足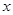 (
(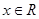 ),则( )
),则( )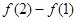 >
>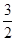
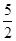
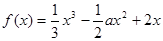 ,讨论
,讨论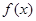 的单调性.
的单调性. .(
.( )
) 有三个零点
有三个零点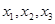 ,且
,且 ,
, ,求函数
,求函数  的单调区间;
的单调区间;  ,
, ,试问:导函数
,试问:导函数 在区间(0,2)内是否有零点,并说明理由.
在区间(0,2)内是否有零点,并说明理由. ,求
,求 的取值范围.
的取值范围.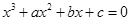 的三个实根分别为一个椭圆,一个抛物线,一个双曲线的离心率,则
的三个实根分别为一个椭圆,一个抛物线,一个双曲线的离心率,则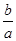 的取值范围________
的取值范围________ 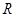 上的函数
上的函数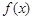 ,对任意
,对任意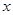 均有
均有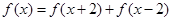 且
且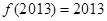 ,则
,则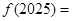 .
.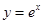 在点
在点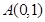 处的切线斜率为 .
处的切线斜率为 .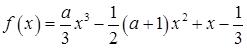 (
(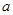
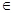 R).
R).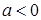 ,求函数
,求函数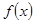 的极值;
的极值;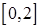 上有两个零点,若存在,求出
上有两个零点,若存在,求出