题目内容
(本题14分)
设函数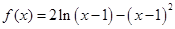 .
.
(1)求函数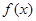 的单调递增区间;
的单调递增区间;
(2)若关于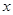 的方程
的方程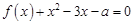 在区间
在区间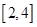 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数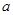 的取值范围.
的取值范围.
设函数
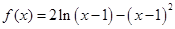 .
.(1)求函数
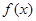 的单调递增区间;
的单调递增区间;(2)若关于
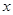 的方程
的方程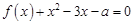 在区间
在区间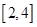 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数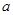 的取值范围.
的取值范围.(Ⅰ)函数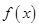 的单调递增区间为
的单调递增区间为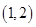 .(Ⅱ)
.(Ⅱ)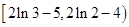 .
.
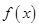 的单调递增区间为
的单调递增区间为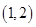 .(Ⅱ)
.(Ⅱ)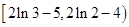 .
. 试题分析:(1)确定出函数的定义域是解决本题的关键,利用导数作为工具,求出该函数的单调递增区间即为f'(x)>0的x的取值区间;
(2)方法一:利用函数思想进行方程根的判定问题是解决本题的关键.构造函数,研究构造函数的性质尤其是单调性,列出该方程有两个相异的实根的不等式组,求出实数a的取值范围.
方法二:先分离变量再构造函数,利用函数的导数为工具研究构造函数的单调性,根据题意列出关于实数a的不等式组进行求解.
解:(Ⅰ)函数
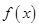 的定义域为
的定义域为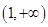 ,………………………1分
,………………………1分∵
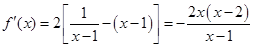 ,………………………2分
,………………………2分∵
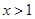 ,则使
,则使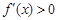 的
的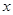 的取值范围为
的取值范围为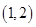 ,
,故函数
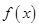 的单调递增区间为
的单调递增区间为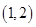 . …………………………4分
. …………………………4分(Ⅱ)方法1:∵
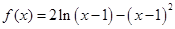 ,
,∴
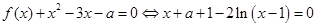 .…………………6分
.…………………6分令
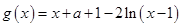 ,
, ∵
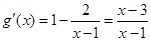 ,且
,且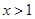 ,
,由
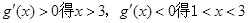 .
.∴
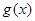 在区间
在区间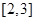 内单调递减,在区间
内单调递减,在区间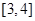 内单调递增,……………………9分
内单调递增,……………………9分故
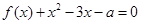 在区间
在区间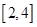 内恰有两个相异实根
内恰有两个相异实根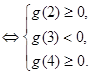 ……11分
……11分即
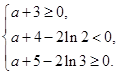 解得:
解得: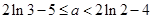 .
.综上所述,
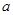 的取值范围是
的取值范围是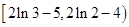 .………………13分
.………………13分方法2:∵
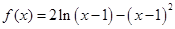 ,
,∴
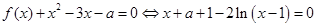 .………………6分
.………………6分即
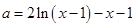 ,
,令
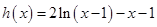 , ∵
, ∵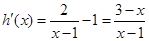 ,且
,且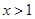 ,
,由
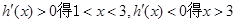 .
.∴
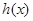 在区间
在区间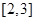 内单调递增,在区间
内单调递增,在区间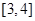 内单调递减.………9分
内单调递减.………9分∵
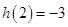 ,
,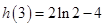 ,
,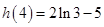 ,
,又
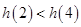 ,故
,故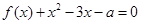 在区间
在区间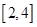 内恰有两个相异实根
内恰有两个相异实根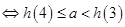 .……11分
.……11分即
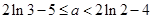 .
.综上所述,
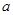 的取值范围是
的取值范围是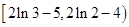 . …………………14分
. …………………14分点评:解决该试题的关键将方程的根的问题转化为函数的图象交点问题。

练习册系列答案
相关题目
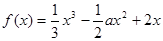 ,讨论
,讨论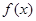 的单调性.
的单调性.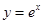 在点
在点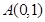 处的切线斜率为 .
处的切线斜率为 .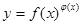 的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得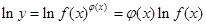 ,两边对
,两边对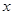 求导数,得
求导数,得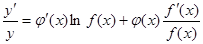 ,于是
,于是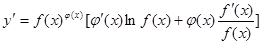 ,运用此方法可以求得函数
,运用此方法可以求得函数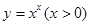 在
在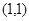 处的切线方程是________________.
处的切线方程是________________.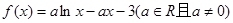 .
.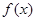 的单调区间;
的单调区间;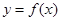 的图像在点
的图像在点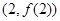 处的切线的倾斜角为
处的切线的倾斜角为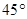 ,问:
,问: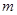 在什么范围取值时,对于任意的
在什么范围取值时,对于任意的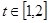 ,函数g(x)=x3 +x2
,函数g(x)=x3 +x2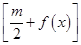 在区间
在区间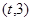 上总存在极值?
上总存在极值?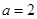 时,设函数
时,设函数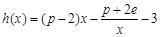 ,若在区间
,若在区间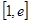 上至少存在一个
上至少存在一个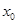 ,
,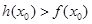 成立,试求实数
成立,试求实数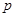 的取值范围.
的取值范围.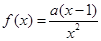 ,其中
,其中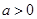 .
.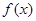 的单调区间;
的单调区间;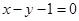 是曲线
是曲线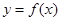 的切线,求实数
的切线,求实数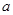 的值;
的值;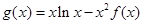 ,求
,求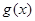 在区间
在区间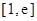 上的最大值.(其中
上的最大值.(其中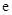 为自然对数的底数)
为自然对数的底数)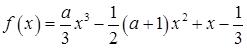 (
(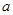
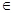 R).
R).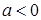 ,求函数
,求函数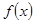 的极值;
的极值;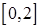 上有两个零点,若存在,求出
上有两个零点,若存在,求出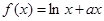
 .
.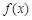 的单调区间;
的单调区间;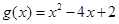 ,若对任意
,若对任意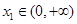 ,均存在
,均存在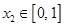 ,使得
,使得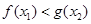 ,求
,求 的取值范围.
的取值范围.