题目内容
已知不等式组
的解集为{x|3<x<4},则a取值范围为( )
|
| A、a≤-2或a≥4 |
| B、-2≤a≤-1 |
| C、-1≤a≤3 |
| D、3≤a≤4 |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:解不等式组中的第一个不等式,可得解集为{x|2<x<-1,或3<x<4}.检验当a<-3,或a=-3时,不满足条件.当a>-3时,解第二个不等式求得它的解集为{x|x<-3,或 x>a},再根据不等式组的解集为的解集为{x|3<x<4},可得a的范围.
解答:
解:解不等式 (x+1)(x+2)(x-3)(x-4)<0,可得-2<x<-1,或3<x<4.
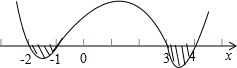
当a<-3时,不等式(x+3)(x-a)>0的解集为{x|x<a,或 x>-3},此时不等式组的解集为{x|-2<x<-1,或3<x<4},不满足条件.
当a=-3时,不等式(x+3)(x-a)>0的解集为{x|x≠-3},此时不等式组的解集为{x|-2<x<-1,或3<x<4},不满足条件.
当a>-3时,不等式(x+3)(x-a)>0的解集为{x|x<-3,或 x>a},再根据不等式组的解集为的解集为{x|3<x<4},
可得-1≤a≤3,
故选:C.

当a<-3时,不等式(x+3)(x-a)>0的解集为{x|x<a,或 x>-3},此时不等式组的解集为{x|-2<x<-1,或3<x<4},不满足条件.
当a=-3时,不等式(x+3)(x-a)>0的解集为{x|x≠-3},此时不等式组的解集为{x|-2<x<-1,或3<x<4},不满足条件.
当a>-3时,不等式(x+3)(x-a)>0的解集为{x|x<-3,或 x>a},再根据不等式组的解集为的解集为{x|3<x<4},
可得-1≤a≤3,
故选:C.
点评:本题主要考查利用穿根法求高次不等式的解集,体现了数形结合、分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
设
<(
)b<(
)a<1,则( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a<b<0 |
| B、b>a>1 |
| C、0<b<a<1 |
| D、0<a<b<1 |
若函数y=x2+bx+3在(-∞,1]上是单调函数,则有( )
| A、b≥2 | B、b≤2 |
| C、b≥-2 | D、b≤-2 |
已知曲线y=2x2+1在点M处的切线斜率为-4,则点M的横坐标是( )
| A、1 | B、-4 | C、-1 | D、不确定 |
 如图所示,C、D、A三点在同一水平线上,AB是塔的中轴线,在C1、D1两处测得塔顶部B处的仰角分别是α=30°和β=60°,如果C、D间的距离是20m,测角仪CC1=DD1=1.5m,则塔高为( )(精确到0.1m)
如图所示,C、D、A三点在同一水平线上,AB是塔的中轴线,在C1、D1两处测得塔顶部B处的仰角分别是α=30°和β=60°,如果C、D间的距离是20m,测角仪CC1=DD1=1.5m,则塔高为( )(精确到0.1m)| A、18.8m |
| B、10.2m |
| C、11.5m |
| D、21.5m |
已知a<b<0,则下列不等式中成立的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知向量m、n满足|
|=2,|
|=3,|m-n|=
,则|
+
|=( )
| m |
| n |
| 17 |
| m |
| n |
A、
| ||
| B、3 | ||
C、
| ||
D、
|