题目内容
已知曲线y=2x2+1在点M处的切线斜率为-4，则点M的横坐标是（ ）
| A、1 | B、-4 | C、-1 | D、不确定 |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：求出函数的导函数，根据曲线在M点处的切线斜率为-4，令导函数等于-4，得到关于x的方程，求出方程的解即为切点的横坐标．
解答：
解：因为y=2x2+1，所以y′=4x，
由曲线在M点的切线斜率为-4，令y′=4x=-4，解得x=-1．
故选：C．
由曲线在M点的切线斜率为-4，令y′=4x=-4，解得x=-1．
故选：C．
点评：此题考查学生切线的几何意义，会利用导数求曲线上在某点处的切线的斜率，是一道基础题．
练习册系列答案
阅读快车系列答案
相关题目
设函数f（x）=log2x，则“a＞b”是“f（a）＞f（b）”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
如果f（x）=mx2+（m-1）x+1在区间（-∞，1]上为减函数，则m的取值范围（ ）
A、（0，
| ||
B、[0，
| ||
C、[0，
| ||
D、（0，
|
已知不等式组
的解集为{x|3＜x＜4}，则a取值范围为（ ）
|
| A、a≤-2或a≥4 |
| B、-2≤a≤-1 |
| C、-1≤a≤3 |
| D、3≤a≤4 |
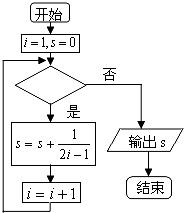如图给出的是计算1+| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2013 |
| A、i≤1006 |
| B、i＞1006 |
| C、i≤1007 |
| D、i＞1007 |
函数y=x2-x，（-1＜x＜4）值域是（ ）
A、[-
| ||
| B、（2，12） | ||
| C、（2，20） | ||
D、[-
|