题目内容
对于函数f(x)定义域中任意的x1,x2(x1≠x2)有如下结论
①f(x1+x2)=f(x1)•f(x2)
②f(x1•x2)=f(x1)+f(x2)
③
<0
④f(
)>
当f(x)=log3x时,上述结论中正确的序号是( )
①f(x1+x2)=f(x1)•f(x2)
②f(x1•x2)=f(x1)+f(x2)
③
| f(x1)-f(x2) |
| x1-x2 |
④f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
当f(x)=log3x时,上述结论中正确的序号是( )
| A、①② | B、②④ | C、①③ | D、③④ |
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:根据对数的运算性质,可以判断①②的真假;根据常用对数函数的单调性,可以判断③的真假;根据常用对数函数图象的形状为凹增的,可以判断④的真假,进而得到答案.
解答:
解:①f(x1+x2)=log3(x1+x2)≠f(x1)f(x2)=log3x1•log3x2,①错误,
②f(x1•x2)=log3(x1•x2)=log3x1log3x2=f(x1)•f(x2),∴②正确.
③满足条件
<0的函数为减函数,∴函数f(x)=log3x为减函数,∴③错误;
④满足条件f(
)>
的函数为凸函数,∴f(x)=log3x为凸函数,∴④正确.
故选:B.
②f(x1•x2)=log3(x1•x2)=log3x1log3x2=f(x1)•f(x2),∴②正确.
③满足条件
| f(x1)-f(x2) |
| x1-x2 |
④满足条件f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
故选:B.
点评:本题主要考查了对数的基本运算性质,对数函数单调性的应用,对数函数图象的形状,熟练掌握对数的图象及性质是解答本题的关键.

练习册系列答案
相关题目
已知角α的终边经过点P(0,-4),则tanα=( )
| A、0 | B、-4 | C、4 | D、不存在 |
设a=20.1,b=ln2,c=log3
,则( )
| 1 |
| 2 |
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、b<a<c |
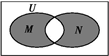 已知全集U=R,集合M={x|y=
已知全集U=R,集合M={x|y=| 3-x2 |
| π |
| 4 |
A、[-3,-
| ||||
B、(1,
| ||||
C、[-3,-
| ||||
D、[-3,-
|
|2x+2|-|2x-2|≤a恒成立,则实数a的取值范围是( )
| A、(-∞,-4) |
| B、[4,+∞) |
| C、[-4,+∞) |
| D、(-4,+∞) |