题目内容
6. 某沿海四个城市A,B,C,D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30$\sqrt{3}$nmile,AD=70$\sqrt{6}$nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发向直线航行,一段时间到达D后,轮船收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ=$\frac{\sqrt{2}}{2}$.
某沿海四个城市A,B,C,D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30$\sqrt{3}$nmile,AD=70$\sqrt{6}$nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发向直线航行,一段时间到达D后,轮船收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ=$\frac{\sqrt{2}}{2}$.
分析 求出AC,计算∠ACD,利用正弦定理再计算∠ADC,故而θ=75°-∠ADC.
解答  解:连结AC,
解:连结AC,
在△ABC中,由余弦定理得:AC2=6400+(40+30$\sqrt{3}$)2-2×$80×(40+30\sqrt{3})×\frac{1}{2}$=7500,
∴AC=50$\sqrt{3}$,
由正弦定理得$\frac{AB}{sin∠ACB}=\frac{AC}{sin∠ABC}$,即$\frac{80}{sin∠ACB}=\frac{50\sqrt{3}}{\frac{\sqrt{3}}{2}}$,
解得sin∠ACB=$\frac{4}{5}$,∴cos∠ACB=$\frac{3}{5}$,
∴sin∠ACD=sin(135°-∠ACB)=$\frac{\sqrt{2}}{2}$×$\frac{3}{5}$+$\frac{\sqrt{2}}{2}$×$\frac{4}{5}$=$\frac{7\sqrt{2}}{10}$,
在△ACD中,由正弦定理得$\frac{AC}{sin∠ADC}=\frac{AD}{sin∠ACD}$,即$\frac{50\sqrt{3}}{sin∠ADC}$=$\frac{70\sqrt{6}}{\frac{7\sqrt{2}}{10}}$,
解得sin∠ADC=$\frac{1}{2}$,∴∠ADC=30°,
∴sinθ=sin(75°-30°)=sin45°=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查了正弦定理,解三角形的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知集合A={1,2,3,4,5},B={3,4,5,6,7},则图中阴影部分表示的集合为( )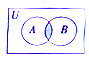

| A. | {1,2,3,4,5} | B. | {3,4,5,6,7} | C. | {1,2,3,4,5,6,7} | D. | {3,4,5} |
11.已知直线l1:(m-4)x-(2m+4)y+2m-4=0与l2:(m-1)x+(m+2)y+1=0,则“m=-2”是“l1∥l2”的( )条件.
| A. | 充要 | B. | 充分不必要 | ||
| C. | 必要不充分 | D. | 既不充分又不必要 |
18.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点为F1、F2,在双曲线上存在点P满足3|$\overrightarrow{P{F_1}}+\overrightarrow{P{F_2}}|≤2|\overrightarrow{{F_1}{F_2}}$|,则双曲线的渐近线的斜率$\frac{b}{a}$的取值范围是( )
| A. | $0<\frac{b}{a}≤\frac{3}{2}$ | B. | $\frac{b}{a}≥\frac{3}{2}$ | C. | $0<\frac{b}{a}≤\frac{{\sqrt{5}}}{2}$ | D. | $\frac{b}{a}≥\frac{{\sqrt{5}}}{2}$ |
15.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左、右焦点分别为F1,F2,点P在双曲线的右支上,且|PF1|=λ|PF2|(λ>1),$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$,双曲线的离心率为$\sqrt{2}$,则λ=( )
| A. | $\sqrt{2}$ | B. | $2+\sqrt{3}$ | C. | $2+\sqrt{2}$ | D. | $2\sqrt{3}$ |