题目内容
椭圆E: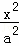 +
+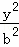 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为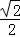 ,且以原点为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+
,且以原点为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+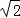 =0相切.
=0相切.
(1)求椭圆E的方程;
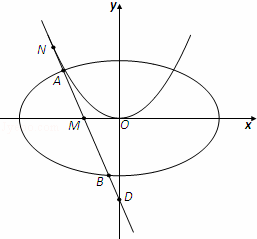
(2)已知直线l过点M(﹣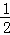 ,0)且与开口向上,顶点在原点的抛物线C切于第二象限的一点N,直线l与椭圆E交于A、B两点,与y轴交于D点,若
,0)且与开口向上,顶点在原点的抛物线C切于第二象限的一点N,直线l与椭圆E交于A、B两点,与y轴交于D点,若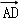 =λ
=λ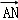 ,
,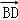 =μ
=μ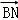 ,且λ+μ=﹣4,求抛物线C的标准方程.
,且λ+μ=﹣4,求抛物线C的标准方程.
解:(1)由题意知e=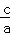 =
=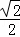 ,
,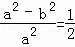 ,
,
即a=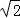 b…(1分)
b…(1分)
又以原点为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+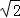 =0相切,
=0相切,
∴b=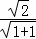 =1,…(2分)
=1,…(2分)
∴a=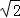 ,
,
故椭圆的方程为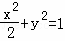 …(4分)
…(4分)
(2)设抛物线C的方程为y=ax2(a>0),直线l与抛物线的切点为N(x0,ax02)
∵y′=2ax,∴切线l的斜率为2ax0,
∴切线方程为y﹣ax02=2ax0(x﹣x0),
∵直线l过点M(﹣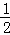 ,0),
,0),
∴﹣ax02=2ax0(﹣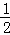 ﹣x0),
﹣x0),
∵点N在第二象限,∴x0<0,
解得x0=﹣1.∴N(﹣1,a).
∴直线l的方程为y=﹣2ax﹣a…(8分)
代入椭圆方程整理得(1+8a2)x2+8a2x+2a2﹣2=0.
设A(x1,y1),B(x2,y2).
∴x1+x2=﹣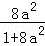 ,x1x2=
,x1x2=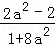 …(10分)
…(10分)
由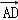 =λ
=λ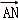 ,
,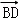 =μ
=μ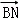 ,
,
得λ=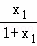 ,μ=
,μ=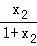
∴λ+μ=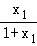 +
+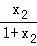 =
=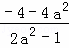 =﹣4,
=﹣4,
∵a>0,
∴a=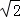
∴抛物线的标准方程为x2=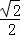 y…(13分)
y…(13分)

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 ).若S1,S2,S3分别是三棱锥D ABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,则( )
).若S1,S2,S3分别是三棱锥D ABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,则( )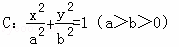 的左右焦点分别为F1,F2,若椭圆C上恰好有6个不同的点P,使得△F1F2P为等腰三角形,则椭圆C的离心率的取值范围是( )
的左右焦点分别为F1,F2,若椭圆C上恰好有6个不同的点P,使得△F1F2P为等腰三角形,则椭圆C的离心率的取值范围是( )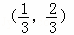 B.
B. 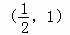 C.
C. 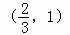 D.
D. 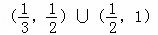
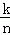 ;
;
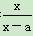 (x≠a).
(x≠a).