题目内容
1．若实数x，y满足（x-4）2+（y-8）2=4，则$\frac{y}{x-4}$的取值范围是（-∞，-$\sqrt{15}$]∪[$\sqrt{15}$，+∞）．分析 设k=$\frac{y-0}{4-0}$=$\frac{y}{x-4}$，则它表示圆（x-4）2+（y-8）2=4上的点M（x，y）与A（4，0）连线的斜率，故当AM为圆的切线时，k取得最值，数形结合，根据圆心C到直线AM的距离等于半径，求得k的值，可得要求式子的取值范围．
解答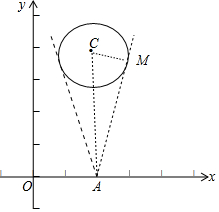 
解：由题意可得$\frac{y}{x-4}$表示圆（x-4）2+（y-8）2=4上的点M（x，y）与A（4，0）连线的斜率，
如图所示，圆心C（4，8），半径为2，当M是直线AM和圆的切点时，
直线AM的斜率 k=$\frac{y-0}{4-0}$=$\frac{y}{x-4}$取得最值，
直线AM的方程为y-0=k（x-4），即kx-y-4k=0，
由圆心C到直线AM的距离等于半径，可得$\frac{|4k-8-4k|}{\sqrt{{k}^{2}+1}}$=2，求得k=±$\sqrt{15}$，
故$\frac{y}{x-4}$的取值范围是 （-∞，-$\sqrt{15}$]∪[$\sqrt{15}$，+∞），
故答案为：（-∞，-$\sqrt{15}$]∪[$\sqrt{15}$，+∞）．
点评 本题主要考查直线的斜率的斜率公式，直线和圆相切的性质，点到直线的距离公式的应用，属于中档题．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
1．设a＞0，b＞0，若2是4a和2b的等比中项，则$\frac{2}{a}$+$\frac{1}{b}$的最小值为（ ）
| A． | $\sqrt{2}$ | B． | 4 | C． | $\frac{9}{2}$ | D． | 5 |
5．将函数f（x）=sin2x的图象向右平移φ（0＜φ＜$\frac{π}{2}$）个单位后得到函数g（x）的图象，若函数g（x）在区间[0，$\frac{π}{3}$]上单调递增，则φ的取值范围是（ ）
| A． | [$\frac{π}{12}$，$\frac{π}{4}$] | B． | [$\frac{π}{6}$，$\frac{5π}{12}$） | C． | [$\frac{π}{6}$，$\frac{π}{3}$] | D． | [$\frac{π}{6}$，$\frac{π}{4}$] |
10．在等腰梯形ABCD中，已知AB∥DC，AB=2，BC=1，∠ABC=60°，动点E和F分别在线段BC和DC上，且$\overrightarrow{BE}=λ\overrightarrow{BC}，\overrightarrow{DF}=\frac{1}{9λ}\overrightarrow{DC}$，则$\overrightarrow{AE}•\overrightarrow{AF}$的最小值为（ ）
| A． | $\frac{27}{18}$ | B． | $\frac{29}{18}$ | C． | $\frac{17}{18}$ | D． | $\frac{13}{18}$ |
11．设a∈R，若函数y=ex+ax，x∈R有小于零的极值点，则实数a的取值范围是（ ）
| A． | （-∞，-1） | B． | （-1，+∞） | C． | （-1，0） | D． | （-∞，0） |