题目内容
15.已知$f(x)={({x+1})^2}\;,\;\;g(x)=\frac{x-1}{x+1}$,则f(x)•g(x)=x2-1,(x≠-1).分析 根据f(x),g(x)的解析式,求出f(x)•g(x)的解析式即可.
解答 解:∵$f(x)={({x+1})^2}\;,\;\;g(x)=\frac{x-1}{x+1}$,
∴f(x)•g(x)=(x+1)(x-1)=x2-1,(x≠-1),
故答案为:x2-1,(x≠-1).
点评 本题考查了求函数的解析式问题,注意函数的定义域问题,是一道基础题.

练习册系列答案
相关题目
6.若一条直线和一个平面内无数条直线垂直,则直线和平面的位置关系是( )
| A. | 垂直 | B. | 平行 | ||
| C. | 相交 | D. | 平行或相交或垂直或在平面内 |
3.若0<a<1,b<-1,则函数f(x)=ax+b的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
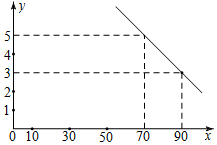 近几年,由于环境的污染,雾霾越来越严重,某环保公司销售一种PM2.5颗粒物防护口罩深受市民欢迎.已知这种口罩的进价为40元,经销过程中测出年销售量y(万件)与销售单价x(元)存在如图所示的一次函数关系,每年销售这种口罩的总开支z(万元)(不含进价)与年销量y(万件)存在函数关系z=10y+42.5.
近几年,由于环境的污染,雾霾越来越严重,某环保公司销售一种PM2.5颗粒物防护口罩深受市民欢迎.已知这种口罩的进价为40元,经销过程中测出年销售量y(万件)与销售单价x(元)存在如图所示的一次函数关系,每年销售这种口罩的总开支z(万元)(不含进价)与年销量y(万件)存在函数关系z=10y+42.5.