题目内容

11．设{an}是由正数构成的等比数列，bn=an+1+an+2，cn=an+an+3，则（　　）
A．bn＞cnB．bn＜cnC．bn≥cnD．bn≤cn

分析 通过作差，利用等比数列的通项公式即可得出．

解答 解：设由正数构成的等比数列{an}的公比为q，bn=an+1+an+2，cn=an+an+3，则cn-bn=an+an+3-（an+1+an+2）=an（1+q3-q-q2）=an（1-q）2（1+q）≥0，
∴cn≥bn．
故选：D．

点评 本题考查了等比数列的通项公式、作差法，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
5．若x，y满足不等式组$\left\{\begin{array}{l}{2x+y-2≥0}\\{x-y+1≥0}\\{6x-y-14≤0}\end{array}\right.$，则z=$\sqrt{（x-1）^{2}+（y-3）^{2}}$的取值范围是（　　）
A．[1，5]B．[$\frac{\sqrt{29}}{3}$，$\sqrt{26}$]C．[$\sqrt{5}$，$\sqrt{26}$]D．[$\frac{\sqrt{2}}{2}$，$\sqrt{26}$]
6．在射击试验中，令X=$\left\{\begin{array}{l}{1，射中}\\{0，未射中}\end{array}\right.$如果射中的概率是0.9，则随机变量的分布列为
X01
P0.10.9
．
3．设f（x）=asin（πx+α）+bcos（πx+β）+7，α．β均为实数，若f（2015）=6，求f（2016）的值．
6．已知$f（x）={log_2}x，g（x）=9-{x^2}，若y=f[{g（x）}]$
（Ⅰ）求函数y=f[g（x）]的解析式；
（Ⅱ）求f[g（1）]，f[g（-1）]的值；
（Ⅲ）判别并证明函数y=f[g（x）]的奇偶性．
16．不等式x2+4x+4≤0的解集为{-2}，不等式$\frac{x-1}{x+1}≤3$的解集为{x|x≤-2或x＞-1}．
3．已知等差数列{an}的前n项和为Sn，且a3=3，S7=28．
（Ⅰ）求{an}的通项公式；
（Ⅱ）若bn=（-1）n•$\frac{{a}_{2n+1}}{{a}_{n}{a}_{n+1}}$，求数列{bn}的前n项和Tn．
20．正方形ABCD中，点A（0，-1），B（2，1），圆D经过正方形的中心且在直线AB的左上方．过点A作圆D的切线，切点为E，F，则直线EF的方程为x-y+2=0．
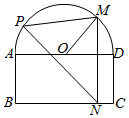1．如图，一个半圆和长方形组成的铁皮，长方形的边AD为半圆的直径，O为半圆的圆心，AB=2，BC=4，现要将此铁皮剪出一个△PMN，其中边MN⊥BC，点P在曲线MAB上运动．
（1）设∠MOD=30°，若PM=PN，求△PMN的面积；
（2）求剪下的铁皮△PMN面积的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网