题目内容
3.设f(x)=asin(πx+α)+bcos(πx+β)+7,α.β均为实数,若f(2015)=6,求f(2016)的值.分析 构造函数g(x)=asin(πx+α)+bcos(πx+β),由f(2015)=6和诱导公式可得g(2015),整体法可得g(2016),再由f(2016)=g(2016)+7可得.
解答 解:构造函数g(x)=asin(πx+α)+bcos(πx+β),则f(x)=g(x)+7,
由f(2015)=g(2015)+7=6可得g(2015)=-1,
即asin(2015π+α)+bcos(2015π+β)=-1,
由诱导公式化简可得asinα+bcosβ=1,
∴g(2016)=asin(2016π+α)+bcos(2016π+β)
=asinα+bcosβ=1,
f(2016)=g(2016)+7=8
点评 本题考查诱导公式的应用,构造函数并整体求解asinα+bcosβ=1是解决问题的关键,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.如果平面α∥平面β,那么下列命题中不正确的是( )
| A. | 平面α内有无数条互相平行的直线平行于平面β | |
| B. | 平面α内仅有两条相交直线平行于平面β | |
| C. | 对于平面α内的任意一条直线,都能在平面β内找到一条直线与它平行 | |
| D. | 平面α内的任意一条直线都不与平面β相交 |
11.若$\frac{sinα+cosα}{cosα-sinα}$=tanβ,α,β∈[0,$\frac{π}{2}$),则β-α等于( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
18.若(1+x)8(x≠0)的展开式的中间三项依次成等差数列,则x的值为( )
| A. | $\frac{1}{2}$或2 | B. | $\frac{1}{2}$或4 | C. | 2或4 | D. | 2或$\frac{1}{4}$ |
4.若函数f(x)是一次函数,且函数图象经过点(0,1),(-1,3),则f(x)的解析式为( )
| A. | f(x)=2x-1 | B. | f(x)=2x+1 | C. | f(x)=-2x-1 | D. | f(x)=-2x+1 |
11.设{an}是由正数构成的等比数列,bn=an+1+an+2,cn=an+an+3,则( )
| A. | bn>cn | B. | bn<cn | C. | bn≥cn | D. | bn≤cn |
8.已知幂函数f(x)=xa在[1,2]上的最大值与最小值的和为5,则α的值为( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | 3 |
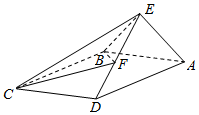 如图,在四棱锥E-ABCD中,底面ABCD是矩形,AB=2,AE⊥平面CDE,AE=DE=2$\sqrt{6}$,F为线段ED上的一点.
如图,在四棱锥E-ABCD中,底面ABCD是矩形,AB=2,AE⊥平面CDE,AE=DE=2$\sqrt{6}$,F为线段ED上的一点.