题目内容
5.若x,y满足不等式组$\left\{\begin{array}{l}{2x+y-2≥0}\\{x-y+1≥0}\\{6x-y-14≤0}\end{array}\right.$,则z=$\sqrt{(x-1)^{2}+(y-3)^{2}}$的取值范围是( )| A. | [1,5] | B. | [$\frac{\sqrt{29}}{3}$,$\sqrt{26}$] | C. | [$\sqrt{5}$,$\sqrt{26}$] | D. | [$\frac{\sqrt{2}}{2}$,$\sqrt{26}$] |
分析 作出可行域,则z表示可行域内的点到(1,3)的距离.根据可行域分别计算距离的最大值,最小值即可.
解答 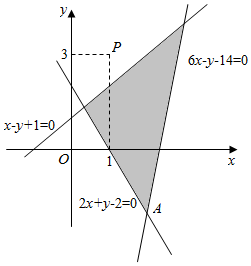 解:作出约束条件表示的可行域如图所示:
解:作出约束条件表示的可行域如图所示:
由z=$\sqrt{(x-1)^{2}+(y-3)^{2}}$的几何意义可知z表示可行域内的点到P(1,3)的距离.
由可行域可知可行域内的点(x,y)到P点(1,3)的最短距离为P到直线x-y+1=0的距离,
最短距离为d=$\frac{|1-3+1|}{\sqrt{2}}=\frac{\sqrt{2}}{2}$,
可行域内的点到P点的最大距离为|PA|,
解方程组$\left\{\begin{array}{l}{2x+y-2=0}\\{6x-y-14=0}\end{array}\right.$,得A(2,-2).
∴|PA|=$\sqrt{(2-1)^{2}+(-2-3)^{2}}$=$\sqrt{26}$.
∴$\frac{\sqrt{2}}{2}$≤z$≤\sqrt{26}$.
故选:D.
点评 本题考查了简单的线性规划,距离公式的应用,属于中档题.

练习册系列答案
相关题目
10.四条直线每两条都相交,且任三条都不交于一点,它们可确定的平面个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.若函数f(x)=logsinα(x2-mx+3m)(α为锐角)在区间[2,+∞)上单凋递减,则实数m的取值围是( )
| A. | (0,4] | B. | (-4,4] | C. | (-∞,4] | D. | [4,+∞) |
14.如果平面α∥平面β,那么下列命题中不正确的是( )
| A. | 平面α内有无数条互相平行的直线平行于平面β | |
| B. | 平面α内仅有两条相交直线平行于平面β | |
| C. | 对于平面α内的任意一条直线,都能在平面β内找到一条直线与它平行 | |
| D. | 平面α内的任意一条直线都不与平面β相交 |
11.设{an}是由正数构成的等比数列,bn=an+1+an+2,cn=an+an+3,则( )
| A. | bn>cn | B. | bn<cn | C. | bn≥cn | D. | bn≤cn |
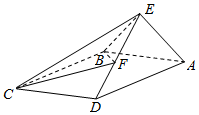 如图,在四棱锥E-ABCD中,底面ABCD是矩形,AB=2,AE⊥平面CDE,AE=DE=2$\sqrt{6}$,F为线段ED上的一点.
如图,在四棱锥E-ABCD中,底面ABCD是矩形,AB=2,AE⊥平面CDE,AE=DE=2$\sqrt{6}$,F为线段ED上的一点.