题目内容
已知函数
(l)求函数 的最小正周期和最大值;
的最小正周期和最大值;
(2)求函数 在
在 上的单调递减区间.
上的单调递减区间.
(1)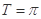 ,
,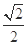 ;(2)
;(2)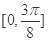 ,
,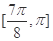 .
.
解析试题分析:(1)先根据三角函数的和角公式、二倍角公式以及差角公式将已知函数化简为: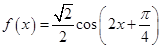 ,然后根据公式
,然后根据公式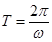 求最小正周期,依据三角函数的图像与性质可知已知函数的最大值;(2)根据余弦函数的图像与性质可知,
求最小正周期,依据三角函数的图像与性质可知已知函数的最大值;(2)根据余弦函数的图像与性质可知,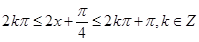 ,解得
,解得 ,即是函数的单调递减区间,由已知
,即是函数的单调递减区间,由已知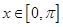 ,可得函数在区间
,可得函数在区间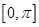 上的单调递减区间是
上的单调递减区间是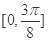 ,
,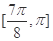 .
.
试题解析: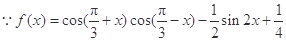
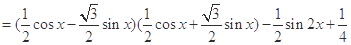
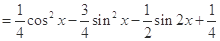
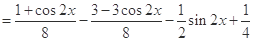
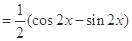
 6分
6分
函数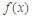 的最小正周期为
的最小正周期为 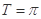 , 7分
, 7分
函数 的最大值为
的最大值为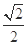 . 8分
. 8分
(2)由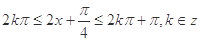 得,
得,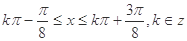 ,
,
函数 的单调递减区间
的单调递减区间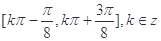 , 10分
, 10分
又因为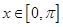 ,则
,则 在
在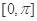 上的单调递减区间为
上的单调递减区间为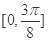 ,
,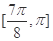 . 12分
. 12分
考点:1.三角函数的图像与性质;2.和角公式与差角公式;3.二倍角公式;4.最小正周期;5.三角函数的单调性与最值

练习册系列答案
相关题目
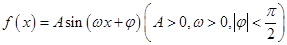 的部分图像如图所示.
的部分图像如图所示.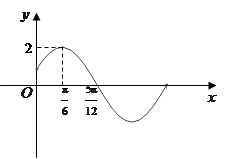
 的解析式;
的解析式;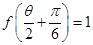 ,
,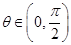 ,求
,求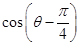 .
.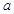
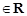 ).
). cosx)(
cosx)(
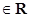 )的最大值为
)的最大值为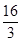 ,求f(x)的最小值;
,求f(x)的最小值;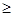 1–a.其中x∈R,x¹kp且x¹kp
1–a.其中x∈R,x¹kp且x¹kp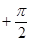 (k∈Z).
(k∈Z).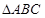 中,
中,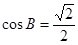 ,
,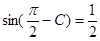 .
.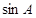 的值;
的值;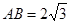 ,求
,求
 ,设函数
,设函数
 的图象关于直线
的图象关于直线 对称,其中常数
对称,其中常数
 的最小正周期;
的最小正周期; 个单位,得到函数
个单位,得到函数 的图像,用五点法作出函数
的图像,用五点法作出函数 的图像.
的图像.
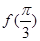 的值;
的值;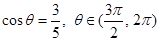 ,求
,求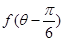 的值.
的值. ,tan(α-β)=-
,tan(α-β)=- .求cosβ的值.
.求cosβ的值. 中,内角
中,内角 所对边长分别为
所对边长分别为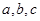 ,
, .
. ;
; ,求
,求 是关于
是关于 的方程
的方程 的两个根.
的两个根. 的值;
的值; 的值.
的值.