题目内容
17．若椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的焦点为F1，F2，点P在椭圆上，且满足|PO|2=|PF1|•|PF2|（ O为坐标原点），则称点P为“●”点，则此椭圆上的“●”点有（ ）| A． | 8个 | B． | 4个 | C． | 2个 | D． | 0个 |
分析 由椭圆中${b^2}＜|P{F_1}||P{F_2}|＜{a^2}$，b≤|PO|≤a，b2≤|PO|2≤a2，因此满足条件的有四个点，
解答 解：${b^2}＜|P{F_1}||P{F_2}|＜{a^2}$，b≤|PO|≤a，b2≤|PO|2≤a2，因此满足条件的有四个点，
故选：B．
点评 本题主要考查椭圆的新定义问题，特别是焦半径的转化问题．考查计算能力．
练习册系列答案
相关题目
8．过M（1，3）引圆x2+y2=2的切线，切点分别为A、B，则△AMB的面积为（ ）
| A． | $\frac{32}{5}$ | B． | 4 | C． | $\frac{16}{5}$ | D． | $\frac{8}{5}$ |
5．已知圆的方程为x2+y2-8x+15=0，若直线y=kx+2上至少存在一点，使得以该点为圆心，半径为1的圆与圆C有公共点，则k的最小值是（ ）
| A． | $-\frac{4}{3}$ | B． | $-\frac{5}{3}$ | C． | $-\frac{3}{5}$ | D． | $-\frac{5}{4}$ |
6．
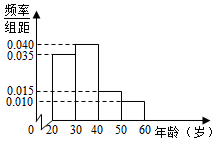某学校有120名教师，且年龄都在20岁到60岁之间，各年龄段人数按分组，其频率分布直方图如图所示，学校要求每名教师都要参加两项培训，培训结束后进行结业考试．已知各年龄段两项培训结业考试成绩优秀的人数如表示，假设两项培训是相互独立的，结业考试成绩也互不影响．
（1）若用分层抽样法从全校教师中抽取一个容量为40的样本，求从年龄段[20，30）抽取的人数；
（2）求全校教师的平均年龄；
（3）随机从年龄段[20，30）和[30，40）内各抽取1人，设这两人中两项培训结业考试成绩都优秀的人数为X，求X的概率分布和数学期望．
某学校有120名教师，且年龄都在20岁到60岁之间，各年龄段人数按分组，其频率分布直方图如图所示，学校要求每名教师都要参加两项培训，培训结束后进行结业考试．已知各年龄段两项培训结业考试成绩优秀的人数如表示，假设两项培训是相互独立的，结业考试成绩也互不影响．| 年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
| [20，30） | 30 | 18 |
| [30，40） | 36 | 24 |
| [40，50） | 12 | 9 |
| [50，60] | 4 | 3 |
（2）求全校教师的平均年龄；
（3）随机从年龄段[20，30）和[30，40）内各抽取1人，设这两人中两项培训结业考试成绩都优秀的人数为X，求X的概率分布和数学期望．
已知F1（-$\sqrt{3}$，0），F2（$\sqrt{3}$，0）为椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，点P在椭圆C上，且△PF1F2面积的最大值为$\sqrt{3}$．