题目内容
12．△ABC的内角A、B、C所对的边分别为a、b、c，若a=1，b+c=$\sqrt{6}$，且cosA=$\frac{1}{4}$，则△ABC的面积为$\frac{\sqrt{15}}{4}$．分析 利用同角三角函数关系式可求sinA，由余弦定理解得bc，利用三角形面积公式即可得解．
解答 解：△ABC中，∵a=1，b+c=$\sqrt{6}$，且cosA=$\frac{1}{4}$，可得：sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{\sqrt{15}}{4}$，
∴由余弦定理a2=b2+c2-2bccosA，可得：1=b2+c2-$\frac{1}{2}$bc=（b+c）2-$\frac{5}{2}$bc=6-$\frac{5}{2}$bc，解得：bc=2．
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}×$2×$\frac{\sqrt{15}}{4}$=$\frac{\sqrt{15}}{4}$．
故答案为：$\frac{\sqrt{15}}{4}$．
点评 本题主要考查了同角三角函数关系式，余弦定理，三角形面积公式的应用，属于基本知识的考查．
练习册系列答案
相关题目
13．下列变换能得到y=cos（x+$\frac{π}{2}$）的图象的有（ ）
①将y=cosx的图象向右平移$\frac{π}{2}$个单位
②将y=cosx的图象向左平移$\frac{π}{2}$个单位
③将y=sinx的图象向右平移π个单位
④将y=sinx的图象向左平移π个单位．
①将y=cosx的图象向右平移$\frac{π}{2}$个单位
②将y=cosx的图象向左平移$\frac{π}{2}$个单位
③将y=sinx的图象向右平移π个单位
④将y=sinx的图象向左平移π个单位．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
20．若存在a∈R，使得|x+a|≤lnx+1在[1，m]上恒成立，则整数m的最大值为（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
7．
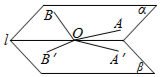如图，小于90°的二面角α-l-β中O∈l，A，B∈α，且∠AOB为钝角，∠A′OB′是∠AOB在β内的射影，则下列结论一定错误的是（ ）
如图，小于90°的二面角α-l-β中O∈l，A，B∈α，且∠AOB为钝角，∠A′OB′是∠AOB在β内的射影，则下列结论一定错误的是（ ）| A． | ∠A′OB′为钝角 | B． | ∠A′OB′＞∠AOB | ||
| C． | ∠AOB+∠AOA′＜π | D． | ∠B′OB+∠BOA+∠AOA′＞π |