题目内容
6.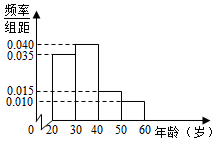 某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.
某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.| 年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
| [20,30) | 30 | 18 |
| [30,40) | 36 | 24 |
| [40,50) | 12 | 9 |
| [50,60] | 4 | 3 |
(2)求全校教师的平均年龄;
(3)随机从年龄段[20,30)和[30,40)内各抽取1人,设这两人中两项培训结业考试成绩都优秀的人数为X,求X的概率分布和数学期望.
分析 (1)由频率分布直方图能求出从年龄段[20,30)抽取的人数.
(2)由频率分布直方图能求出全校教师的平均年龄.
(3)由题设知X的可能取值为0,1,2.分别求出相应的概率,由此能求出X的概率分布列和数学期望.
解答 解:(1)由频率分布直方图知,0.35×40=14.…(2分)
(2)由频率分布直方图得:
全校教师的平均年龄为:
25×0.35+35×0.4+45×0.15+55×0.1=35.…(4分)
(3)∵在年龄段[20,30)内的教师人数为120×0.35=42(人),从该年龄段任取1人,
由表知,此人A项培训结业考试成绩优秀的概率为$\frac{30}{42}=\frac{5}{7}$,
B项培训结业考试成绩优秀的概率为$\frac{18}{42}=\frac{3}{7}$,
∴此人A、B两项培训结业考试成绩都优秀的概率为$\frac{5}{7}×\frac{3}{7}=\frac{15}{49}$,…(6分)
∵在年龄段[30,40)内的教师人数为120×0.4=48(人),
从该年龄段任取1人,由表知,此人A项培训结业考试成绩优秀的概率为$\frac{36}{48}=\frac{3}{4}$,
B项培训结业考试成绩优秀的概率为$\frac{24}{48}=\frac{1}{2}$,
∴此人A、B两项培训结业考试成绩都优秀的概率为$\frac{3}{4}×\frac{1}{2}=\frac{3}{8}$…(8分)
由题设知X的可能取值为0,1,2.
∴$P(X=0)=(1-\frac{15}{49})(1-\frac{3}{8})=\frac{85}{196},P(X=1)=\frac{15}{49}×(1-\frac{3}{8})+(1-\frac{15}{49})×\frac{3}{8}=\frac{177}{392}$,
$P(X=2)=\frac{15}{49}×\frac{3}{8}=\frac{45}{392}$,…(10分)
∴X的概率分布为
| X | 0 | 1 | 2 |
| P | $\frac{85}{196}$ | $\frac{177}{392}$ | $\frac{45}{392}$ |
点评 本题考查频率分布直方图的应用,考查离散型随机变量的求法,是中档题,解题时要认真审题,注意相互独立事件乘法公式的合理运用.

| A. | 8个 | B. | 4个 | C. | 2个 | D. | 0个 |
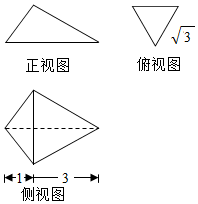
| A. | $\frac{16π}{3}$ | B. | $\frac{32π}{3}$ | C. | 4$\sqrt{3}$ | D. | 16π |
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | -1 |
| A. | y=|tanx| | B. | y=lg$\frac{x+1}{x-1}$ | C. | y=x${\;}^{\frac{1}{3}}$ | D. | y=x-2 |
 某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:
某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图: