题目内容
8.过M(1,3)引圆x2+y2=2的切线,切点分别为A、B,则△AMB的面积为( )| A. | $\frac{32}{5}$ | B. | 4 | C. | $\frac{16}{5}$ | D. | $\frac{8}{5}$ |
分析 作出图象易得sin∠OMB,进而可得cos∠AMB和sin∠AMB=$\frac{4}{5}$,代入三角形的面积公式计算可得.
解答 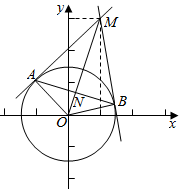 解:如图,由题意可得|OM|=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
解:如图,由题意可得|OM|=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
由勾股定理可得|MA|=|MB|=$\sqrt{O{M}^{2}-O{B}^{2}}$=2$\sqrt{2}$,
故sin∠OMB=$\frac{OB}{OM}$=$\frac{\sqrt{2}}{\sqrt{10}}$=$\frac{\sqrt{5}}{5}$,
∴cos∠AMB=cos2∠OMB=2cos2∠OMB-1=-$\frac{3}{5}$,
故sin∠AMB=$\frac{4}{5}$,三角形面积S=$\frac{1}{2}$×|MA|×|MB|×sin∠AMB=$\frac{16}{5}$,
故选:C.
点评 本题考查圆的切线问题,涉及勾股定理和三角形的面积公式以及三角函数公式,属基础题.

练习册系列答案
相关题目
20.若存在a∈R,使得|x+a|≤lnx+1在[1,m]上恒成立,则整数m的最大值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
17.若椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的焦点为F1,F2,点P在椭圆上,且满足|PO|2=|PF1|•|PF2|( O为坐标原点),则称点P为“●”点,则此椭圆上的“●”点有( )
| A. | 8个 | B. | 4个 | C. | 2个 | D. | 0个 |
18.抛掷一枚硬币,记$X=\left\{\begin{array}{l}1,{\;}^{\;}正面向上\\-1,反面向上\end{array}\right.$,则E(X)=( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | -1 |