Question

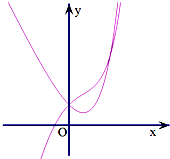已知函数f（x）=e^x-x²的导函数为f′（x），y=f（x）与y=f′（x）在同一直角坐标系下的部分图象如图所示，若方程f′（x）-f（a）=0在x∈（-∞，a]上有两解，则实数a的取值范围是

 

．

Answer 1

考点：利用导数研究函数的单调性

专题：计算题,导数的综合应用

分析：设g（x）=f′（x）-f（a），求出导数，求得g（x）的增区间和减区间，要使满足题意，则需g（a）≥0，g（ln2）＜0，ln2＜a，都成立，设h（a）=2-2ln2-e^a+a²，通过导数，判断单调性，即可得到a的范围．

解答： 解：设g（x）=f′（x）-f（a）=e^x-2x-（e^a-a²），
令g′（x）=e^x-2＞0，则x＞ln2，
所以g（x）在（-∞，ln2）单调递减，
在（ln2，+∞）单调递增，
要使满足题意，
则

g(a)≥0 g(ln2)＜0 ln2＜a

⇒

ea-2a-ea+a2≥0---(1) 2-2ln2-ea+a2＜0--(2) ln2＜a---------(3)

由（1），（3）可知a≥2
设h（a）=2-2ln2-e^a+a²，h′（a）=-e^a+2a＜0在a≥2恒成立，
所以h（a）=2-2ln2-e^a+a²在[2，+∞）上单调递减，
所以h（a）≤h（2）=6-2ln2-e²＜0
所以（2）对任意的a∈R都成立．
综上所述a≥2．
故答案为：[2，+∞）．

点评：本题考查导数的运用：求单调性，考查函数的单调性的运用，考查运算能力，属于中档题．