题目内容

14．已知等差数列{an}的前n项和Sn，且满足${S_{n+1}}={n^2}-n$，则a1=（　　）
A．4B．2C．0D．-2

分析 根据等差数列{an}的前n项和Sn的定义，利用a1=S1，即可求出结果．

解答 解：∵等差数列{an}的前n项和为Sn，
且满足${S_{n+1}}={n^2}-n$，
∴Sn=（n-1）2-（n-1）=n2-3n+2
∴a1=S1=12-3×1+2=0．
故选：C．

点评 本题考查了等差数列前n项和的应用问题，是基础题目．

练习册系列答案
相关题目
19．已知圆C的圆心在射线y=2x-3（x≥0），且与直线y=x+2和y=-x+4都相切．
（1）求圆C的方程；
（2）若P（x，y）是圆C上任意一点，求x+2y的最大值．
20．已知S，A，B，C是球O表面上的点，SA⊥平面ABC，AB⊥BC，SA=AB=2，BC=2$\sqrt{2}$，则球O的表面积等于（　　）
A．4πB．8πC．12πD．16π
2．设全集U={1，2，3，4}，集合A={1，3}，B={2，3}，则B∩∁UA={2}．
9．某水利工程队相应政府号召，计划在韩江边选择一块矩形农田，挖土以加固河堤，为了不影响农民收入，挖土后的农田改造成面积为32400m2的矩形鱼塘，其四周都留有宽3m的路面，问所选的农田的长和宽各为多少时，才能使占有农田的面积最少．
19．若数列{an}成等比数列，其公比为2，则$\frac{2{a}_{2}+{a}_{3}}{2{a}_{4}+{a}_{5}}$=$\frac{1}{4}$．
6．已知集合U={0，1，2，3，4}，A={0，1，2，3}，B={0，2，4}，那么A∩（∁UB）等于（　　）
A．{1}B．{0，1}C．{1，3}D．{0，1，2，3}
3．已知定义域为R的单调减函数f（x）是奇函数，当x＞0时，f（x）=$\frac{x}{3}$-2x．
（Ⅰ）求f（0）的值；
（Ⅱ）求f（x）的解析式；
（Ⅲ）若对任意的t∈R，不等式f（t2-2t）+f（2t2-k）＜0恒成立，求实数k的取值范围．
4．向量$\overrightarrow{e_1}，\;\overrightarrow{e_2}，\;\overrightarrow a，\;\overrightarrow b$在正方形网格中的位置如图所示，则$\overrightarrow a-\overrightarrow b$=（　　）
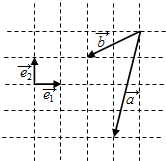
A．$-4\overrightarrow{e_1}-2\overrightarrow{e_2}$B．$-2\overrightarrow{e_1}-4\overrightarrow{e_2}$C．$\overrightarrow{e_1}-3\overrightarrow{e_2}$D．$3\overrightarrow{e_1}-\overrightarrow{e_2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网