题目内容
19.已知圆C的圆心在射线y=2x-3(x≥0),且与直线y=x+2和y=-x+4都相切.(1)求圆C的方程;
(2)若P(x,y)是圆C上任意一点,求x+2y的最大值.
分析 (1)设C(x,2x-3)(x≥0),利用圆C与直线y=x+2和y=-x+4都相切,求出圆心与半径,即可求圆C的方程;
(2)设t=x+2y,则x+2y-t=0,利用圆心到直线的距离d=$\frac{|-1-t|}{\sqrt{5}}$≤2$\sqrt{2}$,即可求x+2y的最大值.
解答 解:(1)设C(x,2x-3)(x≥0),
∵圆C与直线y=x+2和y=-x+4都相切,
∴$\frac{|x-2x+3+2|}{\sqrt{2}}$=$\frac{|x+2x-3-4|}{\sqrt{2}}$,
∵x≥0,∴x=1,
∴C(1,-1),r=2$\sqrt{2}$,
∴圆C的方程(x-1)2+(y+1)2=8;
(2)设t=x+2y,则x+2y-t=0,
圆心到直线的距离d=$\frac{|-1-t|}{\sqrt{5}}$≤2$\sqrt{2}$,
∴-2$\sqrt{10}$-1≤t≤2$\sqrt{10}$+1
∴x+2y的最大值为2$\sqrt{10}$+1.
点评 本题考查圆的方程,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
14.已知数列{an}满足a1=1,a2n=n-an,a2n+1=an+1(n∈N*),则a1+a2+a3+…+a40等于( )
| A. | 222 | B. | 223 | C. | 224 | D. | 225 |
14.已知等差数列{an}的前n项和Sn,且满足${S_{n+1}}={n^2}-n$,则a1=( )
| A. | 4 | B. | 2 | C. | 0 | D. | -2 |
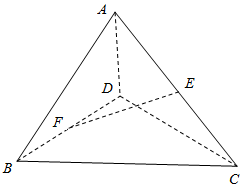 空间四边形ABCD中,AB=8.CD=6,E、F分别是对角线AC,BD的中点,且EF=6.求异面直线AB、CD所成的角的大小.
空间四边形ABCD中,AB=8.CD=6,E、F分别是对角线AC,BD的中点,且EF=6.求异面直线AB、CD所成的角的大小.