题目内容
设函数f(x)＝lnx＋ln(2－x)＋ax(a>0)．
(1)当a＝1时，求f(x)的单调区间；
(2)若f(x)在(0,1]上 的最大值为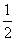
，求a的值．
[解析] 函数f(x)的定义域为(0,2)，f ′(x)＝
－
＋a，
(1)当a＝1时，f ′(x)＝
，所以f(x)的单调递增区间为(0，
)，单调递减区间为(，2)；
(2)当x∈(0,1]时，f ′(x)＝
＋a>0，
即f(x)在(0,1]上单调递增，故f(x)在(0,1]上的最大值为f(1)＝a，因此a＝.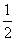
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
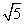km．现要过点P修建一条直线公路BC，将三条公路围成的区域ABC建成一个工业园．为尽量减少耕地占用，问如何确定B点的位置，使得该工业园区的面积最小？并求最小面积．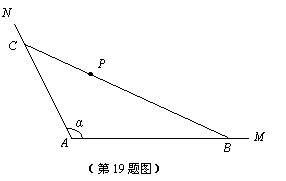
，若0＜x1＜x2＜1，则（ ）
B．
D．无法判断
与
的大小
是定义在
上的非负可导函数，且满足
，对任意正数
，若
，则必有（ ）
B．
C．
D．
是纯虚数，则实数
的值是__ ___ ．
则
．
的部分图象是