题目内容
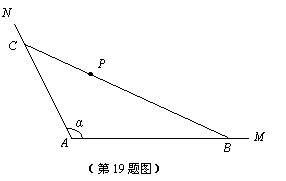
如图(示意),公路AM、AN围成的是一块顶角为α的角形耕地,其中tanα=-2.在该块土地中P处有一小型建筑,经测量,它到公路AM,AN的距离分别为3km,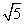 km.现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园.为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.
km.现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园.为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.
 |
解:(方法一)
 如图1,以A为原点,AB为x轴,建立平面直角坐标系.
如图1,以A为原点,AB为x轴,建立平面直角坐标系.
因为tanα=-2,故直线AN的方程是y=-2x.
设点P(x0,y0).
因为点P到AM的距离为3,故y0=3.
由P到直线AN的距离为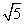 ,
,
得 =
=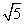 ,解得x0=1或x0=-4(舍去),
,解得x0=1或x0=-4(舍去),
所以点P(1,3).
显然直线BC的斜率存在.设直线BC的方程为y-3=k(x-1),k∈(-2,0).
令y=0得xB=1- .
.
由 解得yC=
解得yC= .
.
设△ABC的面积为S,则S=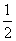 ×xB×yC=
×xB×yC= =-1+
=-1+ .
.
由S¢= =0得k=-
=0得k=- 或k=3.
或k=3.
当-2<k<- 时,S¢<0,S单调递减;当-
时,S¢<0,S单调递减;当- <k<0时,S¢>0,S单调递增
<k<0时,S¢>0,S单调递增
所以当k=- 时,即AB=5时,S取极小值,也为最小值15.
时,即AB=5时,S取极小值,也为最小值15.
答:当AB=5km时,该工业园区的面积最小,最小面积为15km2.
(方法二)
如图1,以A为原点,AB为x轴,建立平面直角坐标系.
因为tanα=-2,故直线AN的方程是y=-2x.
设点P(x0,y0).
因为点P到AM的距离为3,故y0=3.
由P到直线AN的距离为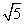 ,
,
得 =
=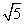 ,解得x0=1或x0=-4(舍去),
,解得x0=1或x0=-4(舍去),
所以点P(1,3).
显然直线BC的斜率存在.设直线BC的方程为y-3=k(x-1),k∈(-2,0).
令y=0得xB=1- .
.
由 解得yC=
解得yC= .
.
设△ABC的面积为S,则S=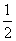 ×xB×yC=
×xB×yC= =-1+
=-1+ .
.
令8k-9=t,则t∈(-25,-9),从而k= .
.
因此S=-1+ =-1+
=-1+ =-1+
=-1+ .
.
因为当t∈(-25,-9)时,t+ ∈(-34,-30],
∈(-34,-30],
当且仅当t=-15时,此时AB=5,34+t+ 的最大值为4.从而S有最小值为15.
的最大值为4.从而S有最小值为15.
答:当AB=5km时,该工业园区的面积最小,最小面积为15km2
(方法三)
如图2,过点P作PE⊥AM,PF⊥AN,垂足为E、F,连接PA.设AB=x,AC=y.
 因为P到AM,AN的距离分别为3,
因为P到AM,AN的距离分别为3,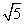 ,
,
即PE=3,PF=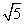 .
.
由S△ABC=S△ABP+S△APC
=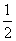 ×x×3+
×x×3+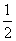 ×y×
×y×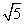 =
=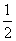 (3x+
(3x+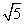 y). ① …… 4分
y). ① …… 4分
因为tana=-2,所以sina= .
.
所以S△ABC=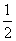 ×x×y×
×x×y×  . ②
. ②
由①②可得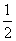 ×x×y×
×x×y×  =
=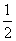 (3x+
(3x+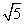 y).
y).
即3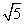 x+5y=2xy. ③
x+5y=2xy. ③
因为3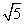 x+5y≥2
x+5y≥2 ,所以 2xy≥2
,所以 2xy≥2 .
.
解得xy≥15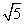 .
.
当且仅当3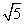 x=5y取“=”,结合③解得x=5,y=3
x=5y取“=”,结合③解得x=5,y=3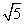 .
.
所以S△ABC=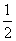 ×x×y×
×x×y×  有最小值15.
有最小值15.
答:当AB=5km时,该工业园区的面积最小,最小面积为15km2.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 表示的平面区域为Ω,其中k≥0,则当Ω的面积最小
表示的平面区域为Ω,其中k≥0,则当Ω的面积最小 的增区间是____________.
的增区间是____________.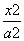 -
-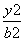 =1(a>0,b>0)的渐近线方程为y=±
=1(a>0,b>0)的渐近线方程为y=±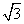 x,则该双曲线的离心率为 .
x,则该双曲线的离心率为 . 上一点P引抛物线准线的垂线,
上一点P引抛物线准线的垂线,
 ,
, ,AD,BE相交于点P.
,AD,BE相交于点P.
 ,求a的值.
,求a的值.