题目内容
函数f(x)=|2-x|+|x-1|的最小值为 .
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:由条件利用绝对值三角不不等式求得f(x)的最小值.
解答:
解:函数f(x)=|2-x|+|x-1|≥|(2-x)+(x-1)|=1,
故答案为:1.
故答案为:1.
点评:本题主要考查绝对值三角不不等式的解法,属于基础题.

练习册系列答案
相关题目
已知不重合的两条直线l,m和不重合的两个平面α,β,下列命题正确的是( )
| A、l∥m,l∥β,则m∥β |
| B、α∩β=m,l?α,则l∥β |
| C、α⊥β,l⊥α,则l∥β |
| D、l⊥m,m⊥β,l⊥α,则α⊥β |
设数列{an}是等比数列,满足an>0,q>1,且a3+a5=20,a2•a6=64,则a6=( )
| A、16 | B、32 | C、42 | D、48 |
采用分层抽样的方法抽取一个容量为45的样本,高一年级被抽取20人,高三年级被抽取10人,高二年级共有300人,则这个学校共有高中生( )人.
| A、1350 | B、675 |
| C、900 | D、450 |
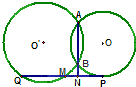 如图,⊙O′和⊙O相交于A和B,PQ切⊙O于P,交⊙O′于Q和M,交AB的延长线于N,MN=3,NQ=15,求PN的长.
如图,⊙O′和⊙O相交于A和B,PQ切⊙O于P,交⊙O′于Q和M,交AB的延长线于N,MN=3,NQ=15,求PN的长.