题目内容
9.已知矩形ABCD的边AB=4,BC=3,若沿对角线AC折叠,使得平面DAC⊥平面BAC,则三棱柱D-ABC的体积$\frac{24}{5}$.分析 过B作BE⊥AC于E,由面面垂直的性质可得BE⊥平面DAC,故BE为棱锥的高,底面为△ACD,代入体积公式计算即可求出体积.
解答 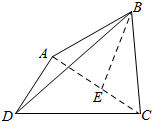 解:过B作BE⊥AC于E,∵AB=4,BC=3,∴AC=5,BE=$\frac{AB•BC}{AC}$=$\frac{12}{5}$,
解:过B作BE⊥AC于E,∵AB=4,BC=3,∴AC=5,BE=$\frac{AB•BC}{AC}$=$\frac{12}{5}$,
∵平面DAC⊥平面BAC,平面DAC∩平面BAC=AC,BE⊥AC,BE?平面ABC,
∴BE⊥平面DAC,
∴V棱锥D-ABC=V棱锥B-ACD=$\frac{1}{3}$S△ACD•BE=$\frac{1}{3}×\frac{1}{2}×3×4×\frac{12}{5}$=$\frac{24}{5}$.
故答案为$\frac{24}{5}$.
点评 本题考查了面面垂直的性质,棱锥的体积计算,是中档题.

练习册系列答案
相关题目
19.某几何体的三视图如图所示,当a+b取最大值时,该几何体体积为( )
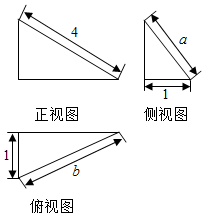

| A. | $\frac{4}{3}$ | B. | $\frac{8}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{16}{9}$ |
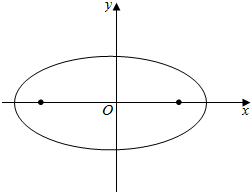 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率 e=$\frac{4}{5}$,且经过点(0,3),左右焦点分别为F1,F2,
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率 e=$\frac{4}{5}$,且经过点(0,3),左右焦点分别为F1,F2,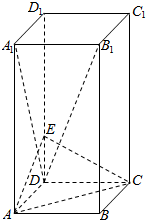 如图,长方体ABCD-A1B1C1D1中,底面ABCD是正方形,AA1=2AB=2,E是DD1上的一点,且满足B1D⊥平面ACE.
如图,长方体ABCD-A1B1C1D1中,底面ABCD是正方形,AA1=2AB=2,E是DD1上的一点,且满足B1D⊥平面ACE. 已知某几何体的三视图如图所示,(图中每一格为1个长度单位)则该几何体的全面积为4+4$\sqrt{5}$.
已知某几何体的三视图如图所示,(图中每一格为1个长度单位)则该几何体的全面积为4+4$\sqrt{5}$.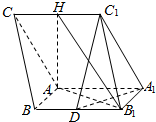 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥侧面ABB1A1,AC=AA1=$\sqrt{2}$AB,∠AA1C1=60°.AB⊥AA1,H为棱CC1的中点,D为BB1的中点.
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥侧面ABB1A1,AC=AA1=$\sqrt{2}$AB,∠AA1C1=60°.AB⊥AA1,H为棱CC1的中点,D为BB1的中点.