题目内容
6.某人打算制定一个长期储蓄计划,每年年初存款2万元,连续储蓄12年.由于资金原因,从第7年年初开始,变更为每年年初存款1万元.若存款利率为每年2%,且上一年年末的本息和共同作为下一年年初的本金,则第13年年初时的本息和约为( )万元(结果精确到0.1).(参考数据:1.026≈1.13,1.0212≈1.27)| A. | 20.09万元 | B. | 20.50万元 | C. | 20.91万元 | D. | 21.33万元 |
分析 由题意第13年年初时的本息和可得:(1+2%)+(1+2%)2+…+(1+2%)6+2[(1+2%)7+(1+2%)8+…+(1+2%)12],利用等比数列的求和公式即可得出.
解答 解:由题意第13年年初时的本息和可得:(1+2%)+(1+2%)2+…+(1+2%)6+2[(1+2%)7+(1+2%)8+…+(1+2%)12]
=$2×\frac{1.02(1-1.0{2}^{12})}{1-1.02}$-$\frac{1.02(1-1.0{2}^{6})}{1-1.02}$
≈20.91,
故选:C.
点评 本题考查了等比数列的求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
16.下列说法中不正确的个数是( )
①“x=1”是“x2-3x+2=0”的必要不充分条件
②命题“?x∈R,cosx≤1”的否定是“?x0∈R,cosx0≥1”
③若一个命题的逆命题为真,则它的否命题一定为真.
①“x=1”是“x2-3x+2=0”的必要不充分条件
②命题“?x∈R,cosx≤1”的否定是“?x0∈R,cosx0≥1”
③若一个命题的逆命题为真,则它的否命题一定为真.
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
17.已知集合 A={x|x2-x-2>0},B={x|1≤x≤3},则图中阴影部分所表示的集合为( )
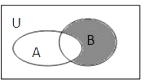

| A. | [1,2) | B. | (1,3] | C. | [1,2] | D. | (2,3] |
11.阅读如图程序框图,如果输出k=5,那么空白的判断框中应填入的条件是( )


| A. | S>-25 | B. | S<-26 | C. | S<-25 | D. | S<-24 |
18.已知i为虚数单位,a∈R,若(a+1)(a-1+i)是纯虚数,则a的值为( )
| A. | -1或1 | B. | 1 | C. | -1 | D. | 3 |
15.已知R为实数集,集合A={x|x>0},B={x|x2-x-2>0},则A∩(∁RB)=( )
| A. | (0,2] | B. | (-1,2) | C. | [-1,2] | D. | [0,4] |