题目内容
4.函数y=f(x)满足对任意x∈R都有f(x+2)=f(-x)成立,且函数y=f(x-1)的图象关于点(1,0)对称,f(1)=4,则f(2016)+f(2017)+f(2018)的值为4.分析 由函数f(x-1)的图象关于(1,0)对称,且由y=f(x-1)向左平移1个单位可得y=f(x)的图象可知,函数y=f(x)的图象关于原点对称,即函数y=f(x)为奇函数,由已知条件可得函数的周期为4,利用所求周期即可求解.
解答 解:∵函数f(x-1)的图象关于(1,0)对称
且把y=f(x-1)向左平移1个单位可得y=f(x)的图象,
∴函数y=f(x)的图象关于(0,0)对称,即函数y=f(x)为奇函数,
∴f(0)=0,
∵f(x+2)=f(-x),又f(-x)=-f(x),
从而可得f(x+2)=-f(x),
将x换成x+2,可得f(x+4)=f(x),
即函数是以4为周期的周期函数,
∴f(2016)=f(504×4)=f(0)=0,
f(2017)=f(504×4+1)=f(1)=4,
f(2018)=f(504×4+2)=f(2)=-f(0)=0,
即有f(2016)+f(2017)+f(2018)=4.
故答案为:4.
点评 本题主要考出了函数的图象的平移及函数图象的对称性的应用,利用赋值求解抽象函数的函数值,函数周期的求解是解答本题的关键所在.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
14.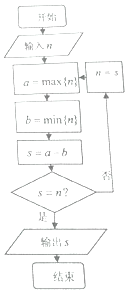 正整数的各数位上的数字重新排列后得到的最大数记为a=max{n},得到的最小数记为b=min{n}(如正整数n=2016,则a=6210,b=0126),执行如图所,示的程序框图,若输入n=2017,则输出的S的值为( )
正整数的各数位上的数字重新排列后得到的最大数记为a=max{n},得到的最小数记为b=min{n}(如正整数n=2016,则a=6210,b=0126),执行如图所,示的程序框图,若输入n=2017,则输出的S的值为( )
 正整数的各数位上的数字重新排列后得到的最大数记为a=max{n},得到的最小数记为b=min{n}(如正整数n=2016,则a=6210,b=0126),执行如图所,示的程序框图,若输入n=2017,则输出的S的值为( )
正整数的各数位上的数字重新排列后得到的最大数记为a=max{n},得到的最小数记为b=min{n}(如正整数n=2016,则a=6210,b=0126),执行如图所,示的程序框图,若输入n=2017,则输出的S的值为( )| A. | 6174 | B. | 7083 | C. | 8341 | D. | 8352 |
12.平行四边形ABCD的两条对角线相交于点M,点P是线段BD上任意一点.若$|\overrightarrow{AB}|=2,|\overrightarrow{AD}|=1$,且∠BAD=60°,则$\overrightarrow{AP}•\overrightarrow{CP}$的取值范围是( )
| A. | $[1,\frac{7}{4}]$ | B. | $[-\frac{7}{4},-1]$ | C. | $[-\sqrt{2},-1]$ | D. | $[-1,\sqrt{2}]$ |
19.设函数f(x)=$\left\{\begin{array}{l}3x-1,x<1\\{2}^{x},x≥1\end{array}\right.$,则满足f(f(a))=2f(a)的a取值范围是( )
| A. | [$\frac{2}{3}$,+∞) | B. | [$\frac{2}{3}$,1] | C. | [1,+∞) | D. | [0,1] |
9.执行如图所示的程序框图,则输出的结果是( )


| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{7}$ | D. | $\frac{6}{7}$ |
16.下列说法中不正确的个数是( )
①“x=1”是“x2-3x+2=0”的必要不充分条件
②命题“?x∈R,cosx≤1”的否定是“?x0∈R,cosx0≥1”
③若一个命题的逆命题为真,则它的否命题一定为真.
①“x=1”是“x2-3x+2=0”的必要不充分条件
②命题“?x∈R,cosx≤1”的否定是“?x0∈R,cosx0≥1”
③若一个命题的逆命题为真,则它的否命题一定为真.
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
13.等比数列中{an},a1,a5为方程x2-10x+16=0的两根,则a3=( )
| A. | 4 | B. | 5 | C. | ±4 | D. | ±5 |
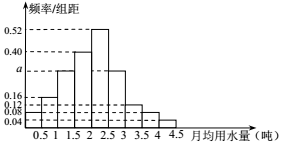 我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过 x 的部分按平价收费,超出 x 的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了 100 位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过 x 的部分按平价收费,超出 x 的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了 100 位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.