题目内容
1．某运动队对A，B，C，D四位运动员进行选拔，只选一人参加比赛，在选拔结果公布前，甲、乙、丙、丁四位教练对这四位运动员预测如下：甲说：“是C或D参加比赛”； 乙说：“是B参加比赛”；丙说：“是A，D都未参加比赛”； 丁说：“是C参加比赛”．若这四位教练中只有两位说的话是对的，则获得参赛的运动员是B．分析 根据题意，依次假设参赛的运动员为A、B、C、D，判断甲、乙、丙、丁的说法的正确性，即可判断．
解答 解：根据题意，A，B，C，D四位运动员进行选拔，只选一人参加比赛，
假设参赛的运动员为A，则甲、乙、丙、丁的说法都错误，不符合题意；
假设参赛的运动员为B，则甲、丁的说法都错误，乙、丙的说法正确，符合题意；
假设参赛的运动员为C，则乙的说法都错误，甲、丙、丁的说法正确，不符合题意；
假设参赛的运动员为D，则乙、丙、丁的说法都错误，甲的说法正确，不符合题意；
故获得参赛的运动员是B；
故选：B．
点评 本题考查了合情推理的问题，注意“这四位教练中只有两位说的话是对”的之一条件．
练习册系列答案
相关题目
11．已知抛物线y2=2px（p＞0）上的点到焦点的距离的最小值为2，过点（0，1）的直线l与抛物线只有一个公共点，则焦点到直线l的距离为（ ）
| A． | 1或$\sqrt{2}$或2 | B． | 1或2或$\sqrt{5}$ | C． | 2或$\sqrt{2}$ | D． | 2或$\sqrt{5}$ |
13．
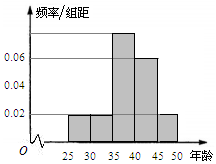某单位280名员工参加“我爱阅读”活动，他们的年龄在25岁至50岁之间，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50），得到的频率分布直方图如图所示．
（ I）现要从年龄低于40岁的员工中用分层抽样的方法抽取12人，则年龄在第1，2，3组的员工人数分别是多少？
（ II）为了交流读书心得，现从上述12人中再随机抽取3人发言，设3人中年龄在[35，40）的人数为ξ，求ξ的数学期望；
（ III）为了估计该单位员工的阅读倾向，现对从该单位所有员工中按性别比例抽取的40人做“是否喜欢阅读国学类书籍”进行调查，调查结果如下表所示：（单位：人）
根据表中数据，我们能否有99%的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系？
附：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$，其中n=a+b+c+d
某单位280名员工参加“我爱阅读”活动，他们的年龄在25岁至50岁之间，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50），得到的频率分布直方图如图所示．（ I）现要从年龄低于40岁的员工中用分层抽样的方法抽取12人，则年龄在第1，2，3组的员工人数分别是多少？
（ II）为了交流读书心得，现从上述12人中再随机抽取3人发言，设3人中年龄在[35，40）的人数为ξ，求ξ的数学期望；
（ III）为了估计该单位员工的阅读倾向，现对从该单位所有员工中按性别比例抽取的40人做“是否喜欢阅读国学类书籍”进行调查，调查结果如下表所示：（单位：人）
| 喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
| 男 | 14 | 4 | 18 |
| 女 | 8 | 14 | 22 |
| 合计 | 22 | 18 | 40 |
附：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$，其中n=a+b+c+d
| P（K2≥k0） | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
11．设集合U={0，1，2，3，4}，A={0，1，3}，B={2，3，4}，则（∁UA）∩B=（ ）
| A． | {2，4} | B． | {2，3，4} | C． | {3} | D． | ∅ |