题目内容
16.函数f(x)=x2-x-2,x∈[-2,2],那么任取一点x0∈[-2,2],使f(x0)≤0的概率是$\frac{3}{4}$.分析 本题是几何概型的考查,只要明确事件对应的区间长度,利用长度比求概率.
解答 解:由题意,本题符合几何概型,区间[-2,2]长度为4,
使f(x0)≤0即x2-x-2≤0的区间为[-1,2],长度为3,
由几何概型公式得到,使f(x0)≤0的概率为$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查了几何概型概率求法;关键是明确事件集合测度,本题是区间长度的比为概率.

练习册系列答案
相关题目
11.正弦函数y=sinx的图象上最高点和最低点之间的最短距离是( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{4+{π}^{2}}$ | D. | 2$\sqrt{1+{π}^{2}}$ |
8.对任意实数x,y,都有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,那么对定义域R上的函数f(x),下列结论正确的是( )
| A. | f(x)是奇函数,又是减函数 | B. | f(x)是奇函数,又是增函数 | ||
| C. | f(x)是偶函数,又是减函数 | D. | f(x)是偶函数,又是增函数 |
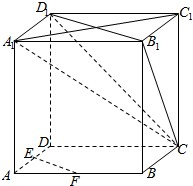 如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AB、AD的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AB、AD的中点.