题目内容
给出下列四个命题:其中所有正确命题的序号为( )
①△ABC中,A>B是sinA>sinB成立的充要条件;
②已知锐角A,B满足tan(A+B)=2tanA,则tanB的最大值是
;
③将y=lnx的图象绕坐标原点O逆时针旋转角θ后第一次与y轴相切,则esinθ=cosθ;
④若函数y=f(x-
)为R上的奇函数,则函数y=f(x)的图象一定关于点F(
,0)成中心对称.
①△ABC中,A>B是sinA>sinB成立的充要条件;
②已知锐角A,B满足tan(A+B)=2tanA,则tanB的最大值是
| ||
| 4 |
③将y=lnx的图象绕坐标原点O逆时针旋转角θ后第一次与y轴相切,则esinθ=cosθ;
④若函数y=f(x-
| 3 |
| 2 |
| 3 |
| 2 |
| A、①②③ | B、②④ |
| C、①③④ | D、①②④ |
考点:命题的真假判断与应用
专题:三角函数的图像与性质,简易逻辑
分析:①△ABC中,由正弦定理可得:sinA>sinB?a>b?A>B,即可判断出;
②已知锐角A,B满足tan(A+B)=2tanA,利用两角和的正切公式展开可得tanB=
,再利用基本不等式的性质即可得出;
③设直线y=kx与曲线y=lnx相切于点P(x0,lnx0),利用导数的几何意义可得x0=e,可得切线方程为y=
x.此切线绕原点逆时针旋转θ后变为y轴,
于是tan(
-θ)=
=
,即可判断出;
④若函数y=f(x-
)为R上的奇函数,则f(-x-
)=-f(x-
),即可判断出.
②已知锐角A,B满足tan(A+B)=2tanA,利用两角和的正切公式展开可得tanB=
| tanA |
| 1+2tan2A |
③设直线y=kx与曲线y=lnx相切于点P(x0,lnx0),利用导数的几何意义可得x0=e,可得切线方程为y=
| 1 |
| e |
于是tan(
| π |
| 2 |
| 1 |
| e |
| cosθ |
| sinθ |
④若函数y=f(x-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:①△ABC中,由正弦定理可得:
=
,sinA>sinB?a>b?A>B,因此正确;
②已知锐角A,B满足tan(A+B)=2tanA,∴
=2tanA,化为tanB=
≤
=
,当且仅当tanA=
时取等号,∴tanB的最大值是
,正确;
③设直线y=kx与曲线y=lnx相切于点P(x0,lnx0),∵y′=
,∴k=
=
,解得x0=e,可得切线方程为y=
x.此切线绕原点逆时针旋转θ后变为y轴,
∴tan(
-θ)=
=
,化为ecosθ=sinθ,因此esinθ=cosθ不正确;
④若函数y=f(x-
)为R上的奇函数,则f(-x-
)=-f(x-
),因此函数y=f(x)的图象一定关于点F(
,0)成中心对称,正确.
综上可得:只有①②④正确.
故选:D.
| a |
| sinA |
| b |
| sinB |
②已知锐角A,B满足tan(A+B)=2tanA,∴
| tanA+tanB |
| 1-tanAtanB |
| tanA |
| 1+2tan2A |
| tanA | ||
2
|
| ||
| 4 |
| ||
| 2 |
| ||
| 4 |
③设直线y=kx与曲线y=lnx相切于点P(x0,lnx0),∵y′=
| 1 |
| x |
| 1 |
| x0 |
| lnx0 |
| x0 |
| 1 |
| e |
∴tan(
| π |
| 2 |
| 1 |
| e |
| cosθ |
| sinθ |
④若函数y=f(x-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
综上可得:只有①②④正确.
故选:D.
点评:本题考查了正弦定理的应用、两角和差的正切公式、基本不等式的性质、利用导数研究切线方程、奇函数的中心对称性,考查了简易逻辑的有关判定,考查了推理能力与计算能力,属于难题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
复数z1=1+i,z2=3+ai,且3z1=z2,则a=( )
| A、0 | B、1 | C、2 | D、3 |
已知双曲线
-y2=1(a>0)的渐近线方程为x±y=0,则双曲的焦距为( )
| x2 |
| a2 |
| A、2 | ||
B、2
| ||
C、
| ||
| D、4 |
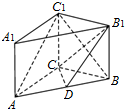 如图,已知在三棱柱ABC-A1B1C1中,AC=4,BC=3,BC1=5,点D在线段AB上,AD=3,BD=2,四边形ACC1A1为正方形.
如图,已知在三棱柱ABC-A1B1C1中,AC=4,BC=3,BC1=5,点D在线段AB上,AD=3,BD=2,四边形ACC1A1为正方形.