题目内容
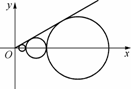
设C1、C2、…、Cn、…是坐标平面上的一列圆，它们的圆心都在轴的正半轴上，且都与直线y＝
x相切，对每一个正整数n，圆Cn都与圆Cn＋1相互外切，以rn表示Cn的半径，已知{rn}为递增数列．
(1) 证明：{rn}为等比数列；
(2) 设r1＝1，求数列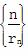
的前n项和.
(1) 证明：将直线y＝
x的倾斜角记为θ，则有tanθ＝，sinθ＝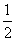
.
设Cn的圆心为(λn，0)，则由题意得
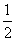＝，得λn＝2rn；同理λn＋1＝2rn＋1，从而λn＋1＝λn＋rn＋rn＋1＝2rn＋1，将λn＝2rn代入，
解得rn＋1＝3rn，故{rn}为公比q＝3的等比数列．
(2) 解：由于rn＝1，q＝3，故rn＝3n－1，从而
＝n×31－n，
记Sn＝
，则有
Sn＝1＋2×3－1＋3×3－2＋…＋n×31－n，①
＝1×3－1＋2×3－2＋…＋(n－1)×31－n＋n×3－n，②
①－②，得
＝1＋3－1＋3－2＋…＋31－n－n×3－n
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
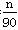(21n－n2－5)(n＝1，2，…，12)，按此预测，在本年度内，需求量超过1.5万件的月份是________．
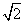，则AC＝________．
的图象，则φ＝________．