题目内容
16.已知△ABC是边长为$2\sqrt{3}$的正三角形,PQ为△ABC外接圆O的一条直径,M为△ABC边上的动点,则$\overrightarrow{PM}•\overrightarrow{MQ}$的最大值是3.分析 以边AB所在直线为x轴,以AB的中点为坐标原点建立平面直角坐标系,
对点M的取值情况分三种情形进行讨论,再运用数量积的坐标表示和二次函数的最值求法,求其最大值.
解答  解:以边AB所在直线为x轴,
解:以边AB所在直线为x轴,
以AB的中点为坐标原点建立平面直角坐标系,如图所示;
∵正三角形ABC的边长为2$\sqrt{3}$,
∴A(-$\sqrt{3}$,0),B($\sqrt{3}$,0),C(0,3),
P(0,-1),Q(0,3),
当点M在边AB上时,设点M(x0,0),则-$\sqrt{3}$≤x0≤$\sqrt{3}$,
∵$\overrightarrow{PM}$=(x0,1),$\overrightarrow{MQ}$=(-x0,3),
∴$\overrightarrow{PM}$•$\overrightarrow{MQ}$=-x02+3,
∵-$\sqrt{3}$≤x0≤$\sqrt{3}$,
∴x0=0时,$\overrightarrow{PM}$•$\overrightarrow{MQ}$取得最大值为3;
当点M在边BC上时,
直线BC的斜率为-$\sqrt{3}$,
直线BC的方程为:$\sqrt{3}$x+y-3=0,
设点M(x0,3-$\sqrt{3}$x0),则0≤x0≤$\sqrt{3}$,
∵$\overrightarrow{PM}$=(x0,4-$\sqrt{3}$x0),$\overrightarrow{MQ}$=(-x0,$\sqrt{3}$x0),
∴$\overrightarrow{PM}$•$\overrightarrow{MQ}$=-4x02+4$\sqrt{3}$x0,
∵0≤x0≤$\sqrt{3}$,
∴x0=0时,$\overrightarrow{PM}$•$\overrightarrow{MQ}$取得最大值为0;
当点M在边AC上时,
直线AC的斜率为$\sqrt{3}$,
∴直线AC的方程为:$\sqrt{3}$x-y+3=0,
设点M(x0,3+$\sqrt{3}$x0),则-$\sqrt{3}$≤x0≤0,
∵$\overrightarrow{PM}$=(x0,4+$\sqrt{3}$x0),$\overrightarrow{MQ}$=(-x0,-$\sqrt{3}$x0),
∴$\overrightarrow{PM}$•$\overrightarrow{MQ}$=-4x02-4$\sqrt{3}$x0,
∵-$\sqrt{3}$≤x0≤0,
∴当x0=-$\frac{\sqrt{3}}{2}$时,$\overrightarrow{PM}$•$\overrightarrow{MQ}$取得最大值为3;
综上,$\overrightarrow{PM}$$•\overrightarrow{MQ}$的最大值为3.
故答案为:3.
点评 本题重点考查了平面向量的基本运算、数量积的运算性质等知识,属于中档题.

 名校课堂系列答案
名校课堂系列答案| 月收入(单位:百元) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 5 | 20 | 30 | 31 | 10 | 4 |
| 赞成人数 | 2 | 14 | 24 | 30 | 7 | 3 |
(2)现从上班中月收入在[10,20)和[60,70)的市民中各随机抽取一个进行跟踪调查,求抽取的两个人恰好对该措施一个赞成一个不赞成的概率.
| A. | -6 | B. | $-\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\sqrt{5}$ | C. | 1 | D. | $\frac{2\sqrt{5}}{5}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | -1+i | B. | -1-i | C. | 1-i | D. | 1+i |
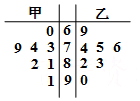 某人到甲、乙两市各7个小区调查空置房情况,调查得到的小区空置房的套数绘成了如图的茎叶图,则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为( )
某人到甲、乙两市各7个小区调查空置房情况,调查得到的小区空置房的套数绘成了如图的茎叶图,则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为( )