题目内容
已知正方形ABCD的边长为1，记以A为起点，其余顶点为终点的向量分别为
，
，
．若i，j∈{1，2，3}且i≠j，则（
i+
j）•
的所有可能取值为 ．
| a1 |
| a2 |
| a3 |
| a |
| a |
| CD |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：如图建立直角坐标系．不妨记以A为起点，其余顶点为终点的向量
，
，
．分别为
，
，
，以C为起点，
，从而得出（
i+
j）•
的所有可能取值．
| a1 |
| a2 |
| a3 |
| AB |
| AC |
| AD |
| CD |
| a |
| a |
| CD |
解答：
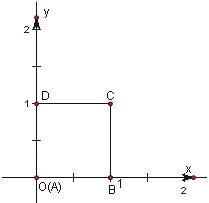解：不妨记以A为起点，其余顶点为终点的向量
，
，
．分别为
=（1，0），
=（1，1），
=（0，1），
以C为起点，
=（0，-1）．如图建立坐标系．
（1）当i=1，j=2时，（
1+
2）•
的=[（1，0）+（1，1）]•（0，-1）=-1；
（2）当i=1，j=3时，则，（
1+
3）•
的=[（1，0）+（0，-1）]•（0，-1）=-1；
（3）当i=2，j=3时，则，（
2+
3）•
的=[（1，1）+（0，1）]•（0，-1）=-2；
（
i+
j）•
的所有可能取值为：-1，-2．
故答案为：-1，-2．
解：不妨记以A为起点，其余顶点为终点的向量| a1 |
| a2 |
| a3 |
| AB |
| AC |
| AD |
以C为起点，
| CD |
（1）当i=1，j=2时，（
| a |
| a |
| CD |
（2）当i=1，j=3时，则，（
| a |
| a |
| CD |
（3）当i=2，j=3时，则，（
| a |
| a |
| CD |
（
| a |
| a |
| CD |
故答案为：-1，-2．
点评：本小题主要考查平面向量坐标表示、平面向量数量积的运算等基本知识，考查考查分类讨论、化归以及数形结合等数学思想方法，考查分析问题、解决问题的能力．
练习册系列答案
相关题目
已知命题p：a2-16≥0，命题q：a+4≤0，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |