题目内容
3.求适合下列条件的圆锥曲线方程:(1)长轴长是短轴长的3倍,经过点(3,0)的椭圆标准方程.
(2)已知抛物线的顶点在原点,准线与其平行线x=2的距离为3,求抛物线标准方程.
分析 (1)由题意,a=3,b=1,即可求出椭圆的标准方程;
(2)由题意,设抛物线的标准方程为y2=2px,准线方程是x=-$\frac{p}{2}$,抛物线的准线方程为x=-$\frac{5}{2}$或$\frac{1}{2}$,求出p,即可求出抛物线的方程.
解答 解:(1)由题意,a=3,b=1,
∴椭圆标准方程为$\frac{x^2}{9}+{y^2}=1$;
(2)由题意,设抛物线的标准方程为y2=2px,准线方程是x=-$\frac{p}{2}$,
∵抛物线的准线方程为x=-$\frac{5}{2}$或$\frac{1}{2}$,
∴$\frac{p}{2}$=-$\frac{5}{2}$或$\frac{1}{2}$,解得p=5或-1,
故所求抛物线的标准方程为y2=10x或y2=-2x.
点评 本题考查椭圆、抛物线的方程与性质,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
11.已知直线m、n与平面α,β,m⊥α,n⊥β,若α⊥β,则m、n的位置关系是( )
| A. | 平行 | B. | 垂直 | C. | 相交 | D. | 异面 |
18.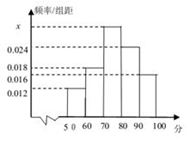 某校为了解高三开学数学考试的情 况,从高三的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60 )的学生人数为6.试根据样本估计“该校高三学生期末数学考试成绩≥70”的 概率为( )
某校为了解高三开学数学考试的情 况,从高三的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60 )的学生人数为6.试根据样本估计“该校高三学生期末数学考试成绩≥70”的 概率为( )
 某校为了解高三开学数学考试的情 况,从高三的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60 )的学生人数为6.试根据样本估计“该校高三学生期末数学考试成绩≥70”的 概率为( )
某校为了解高三开学数学考试的情 况,从高三的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60 )的学生人数为6.试根据样本估计“该校高三学生期末数学考试成绩≥70”的 概率为( )| A. | 0.7 | B. | 0.6 | C. | 0.8 | D. | 0.65 |
8.设变量x,y满足约束条件$\left\{{\begin{array}{l}{x-y≥0}\\{x+y≥1}\\{x≤2}\end{array}}\right.$,则目标函数z=-2x+y的最大值为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | $-\frac{1}{2}$ |