题目内容
甲乙两辆车去同一货场装货物,货场每次只能给一辆车装货物,所以若两辆车同时到达,则需要有一辆车等待.已知甲、乙两车装货物需要的时间都为20分钟,倘若甲、乙两车都在某1小时内到达该货场(在此期间货场没有其他车辆),则至少有一辆车需要等待装货物的概率是 .
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:设现在时间是0,甲乙到场的时间分别是x y,那么就会有0≤x≤60,0≤y≤60,|x-y|如果小于20,就是等待事件,否则不用等待了.由此能求出至少有一辆车需要等待装货物的概率.
解答:
解:设现在时间是0,甲乙到场的时间分别是x y,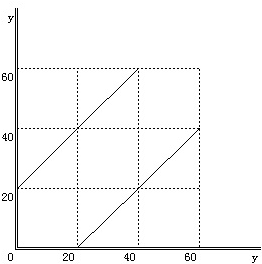
那么就会有:
0≤x≤60,
0≤y≤60,
|x-y|如果小于20,就是等待事件,
否则不用等待了.画出来坐标轴如下图
两条斜直线见的面积是等待,
外面的两个三角形面积是不等待,
∴至少有一辆车需要等待装货物的概率:
p=
=
.

那么就会有:
0≤x≤60,
0≤y≤60,
|x-y|如果小于20,就是等待事件,
否则不用等待了.画出来坐标轴如下图
两条斜直线见的面积是等待,
外面的两个三角形面积是不等待,
∴至少有一辆车需要等待装货物的概率:
p=
60×60-2×
| ||
| 60×60 |
| 5 |
| 9 |
点评:本题考查概率的求法,是中档题,解题时要认真审题,注意几何概型概率计算公式的合理运用.

练习册系列答案
相关题目
下列不等式成立的是( )
| A、1.72.5>1.73 |
| B、0.8-0.1>0.8-0.2 |
| C、1.70.3>0.93.1 |
| D、log21.02<0 |
已知直线x+2y+3=0与直线mx+y+1=0垂直,则m为( )
| A、2 | ||
B、
| ||
C、-
| ||
| D、-2 |
 函数y=f(x)的图象如图所示,在区间[a,b]上可找到n(n≥2)个不同的数x1,x2…xn,使得
函数y=f(x)的图象如图所示,在区间[a,b]上可找到n(n≥2)个不同的数x1,x2…xn,使得
