题目内容
7.下列命题中,真命题是( )| A. | ?x∈R,2x>x2 | B. | ?x∈R,ex<0 | ||
| C. | 若a>b,c>d,则a-c>b-d | D. | ac2>bc2是a>b的充分不必要条件 |
分析 举例说明A、C错误;由指数函数的值域说明B错误;由充分必要条件的判定方法说明D正确.
解答 解:对于A,x=2时,2x=x2,故A错误;
对于B,由指数函数的值域可得ex>0恒成立,故B错误;
对于C,a=2,b=1,c=1,b=-2,满足a>b,c>d,但a-c<b-d,故c错误;
对于D,由ac2>bc2,知c2>0,可得a>b,反之,当c2=0时,由a>0不能得到ac2>bc2,
∴ac2>bc2是a>b的充分不必要条件.
故选:D.
点评 本题考查命题的真假判断与应用,考查了特称命题与全称命题的真假判断,考查了充分必要条件的判定方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.执行如图所示的程序框图,若输入m=4,t=3,则输出y=( )


| A. | 183 | B. | 62 | C. | 61 | D. | 184 |
5.已知函数f(x)=aex-x(a∈R),其中e为自然对数的底数,e=2.71828…
(Ⅰ)判断函数f(x)的单调性,并说明理由
(Ⅱ)若x∈[1,2],不等式f(x)≥e-x恒成立,求a的取值范围.
(Ⅰ)判断函数f(x)的单调性,并说明理由
(Ⅱ)若x∈[1,2],不等式f(x)≥e-x恒成立,求a的取值范围.
12.如图,已知四边形ABCD的直观图是一个边长为1的正方形,则原图形的面积为( )


| A. | $2\sqrt{2}$ | B. | 6 | C. | 8 | D. | 4$\sqrt{2}$+2 |
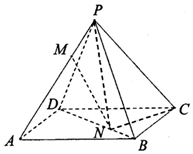 如图,已知正四棱锥P-ABCD中,PA=AB=2,点M,N分别在PA,BD上,且$\frac{PM}{PA}$=$\frac{BN}{BD}$=$\frac{1}{3}$.
如图,已知正四棱锥P-ABCD中,PA=AB=2,点M,N分别在PA,BD上,且$\frac{PM}{PA}$=$\frac{BN}{BD}$=$\frac{1}{3}$.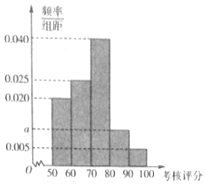 2016年,某省环保部门制定了《省工业企业环境保护标准化建设基本要求及考核评分标准》,为了解本省各家企业对环保的重视情况,从中抽取了40家企业进行考核评分,考核评分均在[50,100]内,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图(满分为100分).
2016年,某省环保部门制定了《省工业企业环境保护标准化建设基本要求及考核评分标准》,为了解本省各家企业对环保的重视情况,从中抽取了40家企业进行考核评分,考核评分均在[50,100]内,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图(满分为100分).