题目内容
19．已知第二象限的角α的终边与单位圆的交点$P（m，\frac{{\sqrt{3}}}{2}）$，则tanα=-$\sqrt{3}$．分析 先求得m的值，再利用任意角的三角函数的定义，求得tanα的值．
解答 解：∵第二象限的角α的终边与单位圆的交点$P（m，\frac{{\sqrt{3}}}{2}）$，∴m＜0，且$\sqrt{{m}^{2}+\frac{3}{4}}$=1，
求得m=-$\frac{1}{2}$，则tanα=$\frac{y}{x}$=$\frac{\frac{\sqrt{3}}{2}}{-\frac{1}{2}}$=-$\sqrt{3}$，
故答案为：$-\sqrt{3}$．
点评 本题主要考查任意角的三角函数的定义，属于基础题．
练习册系列答案
相关题目
9．等差数列{an}的首项为a，公差为1，数列{bn}满足bn=$\frac{{a}_{n}}{{a}_{n}+1}$．若对任意n∈N*，bn≤b6，则实数a的取值范围是（ ）
| A． | （-8，-6） | B． | （-7，-6） | C． | （-6，-5） | D． | （6，7） |
10．已知集合A={0，1，2}，B={x|1＜x＜4}，则集合A∩B=（ ）
| A． | {2} | B． | {1，2} | C． | {0，1，2} | D． | {0，1，2，3} |
14．cos585°的值为（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $-\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $-\frac{{\sqrt{2}}}{2}$ |
11．过点（0，3）且与直线2x+y-5=0垂直的直线方程为（ ）
| A． | 2x+y-3=0 | B． | x+2y-6=0 | C． | x-2y+6=0 | D． | 2x-y+3=0 |
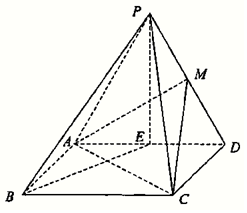如图，在四棱锥P-ABCD中，四边形ABCD是矩形，E，M分别是AD，PD中点，PE⊥BE，PA=PD=AD=2，AB=$\sqrt{2}$．
的图象关于直线
对称，则
的值为（ ）
C．
D．